K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 10 2020
\(\Leftrightarrow\frac{4sin2x+cos2x+17}{3cos2x+sin2x+m+1}-2\ge0\) (tất nhiên là với mọi x)
\(\Leftrightarrow\frac{2sin2x-5cos2x-2m+15}{3cos2x+sin2x+m+1}\ge0\)
TH1: \(\left\{{}\begin{matrix}2sin2x-5cos2x-2m+15\ge0\\3cos2x+sin2x+m+1>0\end{matrix}\right.\) ;\(\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{2}{\sqrt{29}}sin2x-\frac{5}{\sqrt{29}}cos2x\ge\frac{2m-15}{\sqrt{29}}\\\frac{1}{\sqrt{10}}sin2x+\frac{3}{\sqrt{10}}cos2x>\frac{-m-1}{\sqrt{10}}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin\left(2x-a\right)\ge\frac{2m-15}{\sqrt{29}}\\sin\left(2x+b\right)>\frac{-m-1}{\sqrt{10}}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{2m-15}{\sqrt{29}}\le-1\\\frac{-m-1}{\sqrt{10}}< -1\end{matrix}\right.\) tới đây chắc bạn tự giải được
TH2: tương tự:
\(\left\{{}\begin{matrix}2sin2x-5cos2x-2m+15\le0\\3cos2x+sin2x+m+1< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{2m-15}{\sqrt{29}}\ge1\\\frac{-m-1}{\sqrt{10}}>1\end{matrix}\right.\) \(\Leftrightarrow...\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 10 2019
a/ \(-1\le sin2x\le1\Rightarrow-7\le y\le-1\)
b/ \(-1\le cos2x\le1\Rightarrow1\le y\le7\)
c/ \(-1\le sin2x\le1\Rightarrow3\le y\le11\)
d/ \(-1\le cos\left(3x+\frac{\pi}{3}\right)\le1\Rightarrow8\le y\le12\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 6 2019
Đặt \(\left|sinx-cosx\right|=a\) (\(0\le a\le\sqrt{2}\))
\(\Rightarrow1-2sinx.cosx=a^2\Rightarrow1-sin2x=a^2\Rightarrow sin2x=1-a^2\)
Phương trình trở thành:
\(a+4\left(1-a^2\right)=1\Leftrightarrow-4a^2+a+3=0\Rightarrow\left[{}\begin{matrix}a=1\\a=-\frac{3}{4}< 9\left(l\right)\end{matrix}\right.\)
\(\Rightarrow\left|sinx-cosx\right|=1\Leftrightarrow\left|\sqrt{2}sin\left(x-\frac{\pi}{4}\right)\right|=1\)
\(\Leftrightarrow\left|sin\left(x-\frac{\pi}{4}\right)\right|=\frac{\sqrt{2}}{2}\Rightarrow\left[{}\begin{matrix}sin\left(x-\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\\sin\left(x-\frac{\pi}{4}\right)=\frac{-\sqrt{2}}{2}\end{matrix}\right.\) \(\Rightarrow...\)
AH
Akai Haruma
Giáo viên
24 tháng 7 2020
m)
$\sin 4x-\cos ^4x=\cos x-2$
$\Leftrightarrow (\sin ^2x+\cos ^2x)(\sin ^2x-\cos ^2x)=\cos x-2$
$\Leftrightarrow \sin ^2x-\cos ^2x=\cos x-2$
$\Leftrightarrow 1-2\cos ^2x=\cos x-2$
$\Leftrightarrow 2\cos ^2x+\cos x-3=0$
$\Leftrightarrow (2\cos x+3)(\cos x-1)=0$
Nếu $2\cos x+3=0\Rightarrow \cos x=\frac{-3}{2}< -1$ (loại)
Nếu $\cos x-1=0\Rightarrow \cos x=1\Rightarrow x=2k\pi$ với $k$ nguyên
AH
Akai Haruma
Giáo viên
24 tháng 7 2020
k) ĐK:.......
$\tan ^25x=\frac{1}{3}\Rightarrow \tan 5x=\pm \sqrt{\frac{1}{3}}$
$\Rightarrow 5x=k\pi +\tan ^{-1}\frac{\pm 1}{\sqrt{3}}$
$\Rightarrow x=frac{k}{5}\pi +\tan ^{-1}\frac{\pm 1}{\sqrt{3}}$ với $k$ nguyên.
Số đẹp hơn thì có thể giải như sau:
$PT \Leftrightarrow \frac{\sin ^25x}{\cos ^25x}=\frac{1}{3}$
$\Rightarrow 3\sin ^25x=\cos ^25x$
$\Rightarrow 4\\sin ^25x=1\Rightarrow \sin 5x=\pm \frac{1}{2}$
$\Rightarrow x=\frac{k\pi}{5}\pm \frac{\pi}{30}$ với $k$ nguyên.
30 tháng 7 2019
đúng y như trong đề luôn mà bạn , hay là bạn có tính sai chỗ nào đó rồi không
KN
0
TV
0
N
1
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 7 2020
a/
\(\Leftrightarrow\left(sinx-1\right)\left(sinx-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=1\\sinx=4\left(vn\right)\end{matrix}\right.\) \(\Rightarrow x=\frac{\pi}{2}+k2\pi\)
b/
\(\Leftrightarrow\left(cos2x-1\right)\left(2cosx-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=1\\cosx=\frac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pm\frac{\pi}{3}+k2\pi\end{matrix}\right.\)
c/
\(\Leftrightarrow\left(sin3x-\frac{3}{4}\right)^2+\frac{7}{16}=0\)
Vế trái luôn dương nên pt vô nghiệm
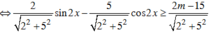
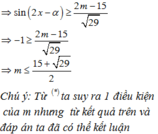
Pt\(\Leftrightarrow3\left(cos^2x-sin^2x\right)-8.sinx.cosx=sin^2x+cos^2x\)
\(\Leftrightarrow2cos^2x-8sinx.cosx-4sin^2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\left(2+\sqrt{6}\right)sinx\\cosx=\left(2-\sqrt{6}\right)sinx\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=\dfrac{1}{2+\sqrt{6}}\\tanx=\dfrac{1}{2-\sqrt{6}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=arc.tan\left(\dfrac{1}{2+\sqrt{6}}\right)+k\pi\\x=arc.tan\left(\dfrac{1}{2-\sqrt{6}}\right)+k\pi\end{matrix}\right.\), k nguyên
Vậy...