Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(x^2-3x-6+4=0\)
\(\Leftrightarrow x^2-3x-2=0\)
Ta có : \(\left(-3\right)^2-4.\left(-2\right)=9+8=17>0\)
Nên có 2 nghiệm phân biệt
\(x_1=\frac{3-\sqrt{17}}{2};x_2=\frac{3+\sqrt{17}}{2}\)
b, Để PT có nghiệm thì \(\Delta=0\)
\(\Leftrightarrow b^2-4ac=0\)
\(\Leftrightarrow\left(-3\right)^2-4\left(-m+4\right)=0\)
\(\Leftrightarrow9+4m-16=0\)
\(\Leftrightarrow7+4m=0\)
\(\Leftrightarrow m=-\frac{7}{4}\)
Vậy => m = -7/4
c, Ko rõ

a) Ta có:Δ =(-7)2 -4.2.2 =49 -16 =33 >0
Phương trình có 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 =-b/a =7/2 ;x1x2 =c/a =2/2 =1
b) c = -16 suy ra ac < 0
Phương trình có 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 =-b/a =-2/5 ;x1x2 =c/a =-16/5
c) Ta có: Δ’ = 22 – (2 -√3 )(2 + √2 ) =4 -4 - 2√2 +2√3 +√6
= 2√3 - 2√2 +√6 >0
Phương trình 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
d) Ta có : Δ = (-3)2 -4.1,4.1,2 =9 – 6,72 =2,28 >0
Phương trình có 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 = -b/a = 3/(1.4) = 30/14 = 15/7 ; x1x2 = c/a = (1.2)/(1.4) = 12/14 = 6/7
Ta có: Δ = 12 -4.5.2 = 1 - 40 = -39 < 0

2:
\(A=\dfrac{x_2-1+x_1-1}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{3-2}{-7-3+1}=\dfrac{1}{-9}=\dfrac{-1}{9}\)
B=(x1+x2)^2-2x1x2
=3^2-2*(-7)
=9+14=23
C=căn (x1+x2)^2-4x1x2
=căn 3^2-4*(-7)=căn 9+28=căn 27
D=(x1^2+x2^2)^2-2(x1x2)^2
=23^2-2*(-7)^2
=23^2-2*49=431
D=9x1x2+3(x1^2+x2^2)+x1x2
=10x1x2+3*23
=69+10*(-7)=-1

5x4 + 2x2 – 16 = 10 – x2
⇔ 5x4 + 2x2 – 16 – 10 + x2 = 0
⇔ 5x4 + 3x2 – 26 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : 5t2 + 3t – 26 = 0 (2)
Giải (2) :
Có a = 5 ; b = 3 ; c = -26
⇒ Δ = 32 – 4.5.(-26) = 529 > 0
⇒ Phương trình có hai nghiệm phân biệt
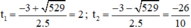
Đối chiếu điều kiện chỉ có t1 = 2 thỏa mãn
+ Với t = 2 ⇒ x2 = 2 ⇒ x = √2 hoặc x = -√2.
Vậy phương trình (1) có tập nghiệm S = {-√2; √2}

a) \(\left(x^2-3x\right)\left(x^2+7x+10\right)=216\Rightarrow x\left(x-3\right)\left(x+2\right)\left(x+5\right)=216\)
\(\Rightarrow x\left(x+2\right)\left(x-3\right)\left(x+5\right)=216\Rightarrow\left(x^2+2x\right)\left(x^2+2x-15\right)=216\)
Đặt \(t=x^2+2x\Rightarrow\) pt trở thành \(t\left(t-15\right)=216\Rightarrow t^2-15t-216=0\)
\(\Rightarrow\left(t+9\right)\left(t-24\right)=0\Rightarrow\left[{}\begin{matrix}t=-9\\t=24\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x^2+2x=-9\\x^2+2x=24\end{matrix}\right.\)
\(TH_1:x^2+2x=-9\Rightarrow x^2+2x+9=0\Rightarrow\left(x+1\right)^2+8=0\) (vô lý)
\(TH_2:x^2+2x=24\Rightarrow x^2+2x-24=0\Rightarrow\left(x-4\right)\left(x+6\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-6\end{matrix}\right.\)
b) \(\left(2x^2-7x+3\right)\left(2x^2+x-3\right)+9=0\)
\(\Rightarrow\left(x-3\right)\left(2x-1\right)\left(x-1\right)\left(2x+3\right)+9=0\)
\(\Rightarrow\left(x-3\right)\left(2x+3\right)\left(x-1\right)\left(2x-1\right)+9=0\)
\(\Rightarrow\left(2x^2-3x-9\right)\left(2x^2-3x+1\right)+9=0\)
Đặt \(t=2x^2-3x-9\Rightarrow\) pt trở thành \(t\left(t+10\right)+9=0\)
\(\Rightarrow t^2+10t+9=0\Rightarrow\left(t+1\right)\left(t+9\right)=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-9\end{matrix}\right.\)
\(TH_1:t=-1\Rightarrow2x^2-3x-9=-1\Rightarrow2x^2-3x-8=0\)
\(\Delta=\left(-3\right)^2-4\left(-8\right).2=73\Rightarrow\left[{}\begin{matrix}x=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{3-\sqrt{73}}{4}\\x=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{3+\sqrt{73}}{4}\end{matrix}\right.\)
\(TH_2:t=-9\Rightarrow2x^2-3x-9=-9\Rightarrow2x^2-3x=0\Rightarrow x\left(2x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)

a) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0
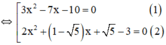
+ Giải (1):
3 x 2 – 7 x – 10 = 0
Có a = 3; b = -7; c = -10
⇒ a – b + c = 0
⇒ (1) có hai nghiệm x 1 = - 1 v à x 2 = - c / a = 10 / 3 .
+ Giải (2):
2 x 2 + ( 1 - √ 5 ) x + √ 5 - 3 = 0
Có a = 2; b = 1 - √5; c = √5 - 3
⇒ a + b + c = 0
⇒ (2) có hai nghiệm:
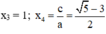
Vậy phương trình có tập nghiệm 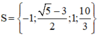
b)
x 3 + 3 x 2 - 2 x - 6 = 0 ⇔ x 3 + 3 x 2 - ( 2 x + 6 ) = 0 ⇔ x 2 ( x + 3 ) - 2 ( x + 3 ) = 0 ⇔ x 2 - 2 ( x + 3 ) = 0
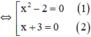
+ Giải (1): x 2 – 2 = 0 ⇔ x 2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
c)
x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x ⇔ x 2 − 1 ( 0 , 6 x + 1 ) = x ⋅ ( 0 , 6 x + 1 ) ⇔ x 2 − 1 ( 0 , 6 x + 1 ) − x ( 0 , 6 x + 1 ) = 0 ⇔ ( 0 , 6 x + 1 ) x 2 − 1 − x = 0
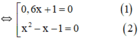
+ Giải (1): 0,6x + 1 = 0 ⇔ 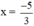
+ Giải (2):
x 2 – x – 1 = 0
Có a = 1; b = -1; c = -1
⇒ Δ = ( - 1 ) 2 – 4 . 1 . ( - 1 ) = 5 > 0
⇒ (2) có hai nghiệm 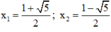
Vậy phương trình có tập nghiệm 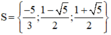
d)
x 2 + 2 x − 5 2 = x 2 − x + 5 2 ⇔ x 2 + 2 x − 5 2 − x 2 − x + 5 2 = 0 ⇔ x 2 + 2 x − 5 − x 2 − x + 5 ⋅ x 2 + 2 x − 5 + x 2 − x + 5 = 0 ⇔ ( 3 x − 10 ) 2 x 2 + x = 0
⇔ (3x-10).x.(2x+1)=0
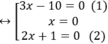
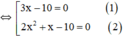
+ Giải (1): 3x – 10 = 0 ⇔ 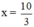
+ Giải (2):
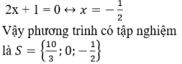

a) Phương trình 7x2 -9x +2 = 0 có hệ số a = 7, b = -9, c = 2
Ta có: a + b + c = 7 + (-9) + 2 = 0
Suy ra nghiệm của phương trình là x1 = 1, x2 = c/a = 2/7
b) Phương trình 23x2 - 9x – 32 = 0 có hệ số a = 23, b = -9, c = -32
Ta có: a –b +c =23 – (-9) +(-32) =0
Suy ra nghiệm của phương trình là x1= -1, x2 = -c/a = -(-32)/23 = 32/23
c. Phương trình 1975x2 + 4x -1979 = 0 có hệ số a = 1975, b = 4, c = -1979
Ta có: a +b +c =1975 + 4 + (-1979) = 0
Suy ra nghiệm của phương trình là x1 = 1, x2 = c/a = -1979/1975
d) Phương trình (5 +√2 )x2 + (5 - √2 )x -10 = 0 có hệ số
a =5 +√2 , b = 5 - √2 , c = -10
Ta có: a +b +c =5 +√2 +5 - √2 +(-10)=0
Suy ra nghiệm của phương trình là x1 = 1 , x2 = ca = (-10)/(5+ √2)
e. Phương trình 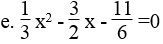
Ta có: a –b +c =2 – (-9) +(-11) =0
Suy ra nghiệm của phương trình là x1=-1 , x2 = -c/a = -(-11)/2 =11/2
f. Phương trình 31,1x2 – 50,9x + 19,8 = 0 ⇔ 311x2 – 509x +198 = 0 có hệ số a = 311, b = -509, c = 198
Ta có: a + b + c = 311 + (-509) + 198 = 0
Suy ra nghiệm của phương trình là x1 = 1 , x2 = c/a = 198/311

a) 2 x 2 – 17 x + 1 = 0
Có a = 2; b = -17; c = 1
Δ = b 2 – 4 a c = ( - 17 ) 2 – 4 . 2 . 1 = 281 > 0 .
Theo hệ thức Vi-et: phương trình có hai nghiệm x1; x2 thỏa mãn:
x 1 + x 2 = − b / a = 17 / 2 x 1 x 2 = c / a = 1 / 2
b) 5 x 2 – x – 35 = 0
Có a = 5 ; b = -1 ; c = -35 ;
Δ = b 2 – 4 a c = ( - 1 ) 2 – 4 . 5 . ( - 35 ) = 701 > 0
Theo hệ thức Vi-et, phương trình có hai nghiệm x1; x2 thỏa mãn:
x 1 + x 2 = − b / a = 1 / 5 x 1 ⋅ x 2 = c / a = − 35 / 5 = − 7
c) 8 x 2 – x + 1 = 0
Có a = 8 ; b = -1 ; c = 1
Δ = b 2 – 4 a c = ( - 1 ) 2 – 4 . 8 . 1 = - 31 < 0
Phương trình vô nghiệm nên không tồn tại x1 ; x2.
d) 25 x 2 + 10 x + 1 = 0
Có a = 25 ; b = 10 ; c = 1
Δ = b 2 – 4 a c = 10 2 – 4 . 25 . 1 = 0
Khi đó theo hệ thức Vi-et có:
x 1 + x 2 = − b / a = − 10 / 25 = − 2 / 5 x 1 x 2 = c / a = 1 / 25
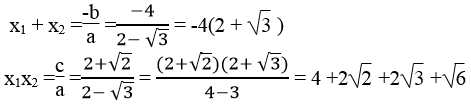
giup mình voi huhu
a) Đặt \(x^2=a\left(a\ge0\right)\)
Ta có: \(2x^4-7x^2+4=0\)
Suy ra: \(2a^2-7a+4=0\)
\(\Delta=49-4\cdot2\cdot4=49-32=17\)
Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}a_1=\dfrac{7-\sqrt{17}}{4}\left(nhận\right)\\a_2=\dfrac{-7+\sqrt{17}}{4}\left(loại\right)\end{matrix}\right.\)
Suy ra: \(x^2=\dfrac{7-\sqrt{17}}{4}\)
\(\Leftrightarrow x=\pm\dfrac{\sqrt{7-\sqrt{17}}}{2}\)
Vậy: \(S=\left\{\dfrac{\sqrt{7-\sqrt{17}}}{2};-\dfrac{\sqrt{7-\sqrt{17}}}{2}\right\}\)