
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 1:
Dễ thấy phương trình có x=2 là 1 nghiệm.
Mặt khác ta có: vế trái luôn nghịch biến do
Vậy phương trình có nghiệm duy nhất x=2
Câu 2:
Áp dụng bất đẳng thức Côsi ta có:
Dễ thấy chỉ xảy ra khi
Mặt khác khi thay x=2 vào vế trái được VT bằng
Vậy kết luận phương trình đã cho vô nghiệm.
Câu 3:
Tương tự phương pháp như câu 2 ta có:
Vế phải
mà
Vậy nên chỉ có thể xảy ra khi
Mặt khác ta có để
Thay x=0 vào (1) được (Thoả mãn)
Vậy phương trình đã cho có nghiệm x=0
Câu 4
Điều kiện là mẫu khác 0 hay x khác
Với điều kiện trên ta có:%20%5CLeftrightarrow%20(2%5E%7Bx%7D)%5E%7B3%7D-5(2%5E%7Bx%7D)%5E%7B2%7D+2%5E%7Bx%7D+10=0)
Bạn đặtta được phương trình sau
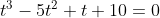
Giải phương trình được,
(loại vì t>0)
Vậy cuối cùng giải ra nghiệm của phương trình là:và

\(x^2+x^4-8^2+16\)
\(=x^{2+4}-8^2+4^2\)
\(=x^6-64+16\)
\(=x^2-48\)
\(=\left(x-\sqrt{48}\right)\left(x+\sqrt{48}\right)\)

ĐẶT x-1=a , x+3=b (a,b cùng dấu)
\(PT\Leftrightarrow ab+2a\sqrt{\frac{b}{a}}=8\)
\(\Leftrightarrow2a\sqrt{\frac{b}{a}}=8-ab\)
\(\Leftrightarrow4a^2\frac{b}{a}=64-16ab+a^2b^2\)
\(\Leftrightarrow a^2b^2-20ab+64=0\)
\(\Leftrightarrow\left(ab-10\right)^2-36=0\)
\(\Leftrightarrow\left(ab-4\right)\left(ab-16\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}ab=4\\ab=16\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x-1\right)\left(x+3\right)=4\\\left(x-1\right)\left(x+3\right)=16\end{cases}}\)
Đến đây đơn giản rồi bn tự giải nhé
ĐK:....\(\frac{x+3}{x-1}\ge0\)
<=> \(\left(x-1\right)\left(x+3\right)+2\sqrt{\left(x-1\right)\left(x+3\right)}+1=9\)
<=> \(\left(\sqrt{\left(x-1\right)\left(x+3\right)}+1\right)^2=9\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{\left(x-1\right)\left(x+3\right)}=2\\\sqrt{\left(x-1\right)\left(x+3\right)}=-4\left(loai\right)\end{cases}}\)
\(\Leftrightarrow\left(x-1\right)\left(x+3\right)=4\)
Em tự làm tiếp nhé

a) căn(2x+5) - căn(3-x) = x2 -5x + 8
Điều kiện : \(-\frac{5}{2}\Leftarrow x\Leftarrow3\)
căn(2x+5) - căn(3-x) = x^2-5x+8
\(\Leftrightarrow\)[căn(2x+5)-3]-[căn(3-x)-1]=x2 -5x+6
nhân liên hợp
\(\Leftrightarrow\)(2x+5-9) / [căn(2x+5)+3] -(3-x-1) / [căn (3-x)+1]=(x-2)(x-3)
\(\Leftrightarrow\)(2x-4) / [căn (2x+5)+3] -(2-x) / [ căn (3-x)+1]-(x-2)(x-3)=0
\(\Leftrightarrow\)(x-2).M=0
\(\Leftrightarrow\)x=2 hoặc M=0
M=2 / [căn(2x+5)+3]+1 / [căn(3-x)+1]-x+3
2/[can(2x+5)+3]+1/[can(3-x)+1]>0 voi moi x
voi -5/2<=x<=3 <->3-x thuoc[0;11/2]
nen M>0
vay x=2
b/ 2+ căn(3-8x) = 6x + căn(4x-1)
dk[1/4;8/3]
6x-2+căn(4x-1)-căn(3-8x)=0
<->2(3x-1)+(4x-1-3+8x)/[căn(4x-1)+căn(...
<->2(3x-1)+(12x-4)/[căn(4x-1)+căn(3-8x...
<->2(3x-1)+4(3x-1)/[căn(4x-1)+căn(3-8x...
<->(3x-1){2+4/[căn(4x-1)+căn(3-8x)]}=0
2+4/[căn(4x-1)+căn(3-8x)>0
nen 3x-1=0
x=1/3
a) căn(2x+5) - căn(3-x) = x^2-5x+8
dkxd -5/2<=x<=3
căn(2x+5) - căn(3-x) = x^2-5x+8
<->[can(2x+5)-3]-[can(3-x)-1]=x^2-5x+6
nhan lien hop
<->(2x+5-9)/[can(2x+5)+3] -(3-x-1)/[can(3-x)+1]=(x-2)(x-3)
<->(2x-4)/[can(2x+5)+3] -(2-x)/[can(3-x)+1]-(x-2)(x-3)=0
<->(x-2).M=0
<->x=2 hoac M=0
M=2/[can(2x+5)+3]+1/[can(3-x)+1]-x+3
2/[can(2x+5)+3]+1/[can(3-x)+1]>0 voi moi x
voi -5/2<=x<=3 <->3-x thuoc[0;11/2]
nen M>0
vay x=2
b/ 2+ căn(3-8x) = 6x + căn(4x-1)
dk[1/4;8/3]
6x-2+căn(4x-1)-căn(3-8x)=0
<->2(3x-1)+(4x-1-3+8x)/[căn(4x-1)+căn(...
<->2(3x-1)+(12x-4)/[căn(4x-1)+căn(3-8x...
<->2(3x-1)+4(3x-1)/[căn(4x-1)+căn(3-8x...
<->(3x-1){2+4/[căn(4x-1)+căn(3-8x)]}=0
2+4/[căn(4x-1)+căn(3-8x)>0
nen 3x-1=0
x=1/3

cái pt thứ 2 bạn nhân 2 vế vs x
Sau đó chuyển hết sang 1 vế,,,dùng máy băm nghiệm


\(\sqrt{x+4\sqrt{x-1}+3}-\sqrt{4x+4\sqrt{x-1}-3}=1\)(đk:\(1\le x< 2\)) Lý do có điều kiện này là nhờ vào việc VT=1>0
\(\Leftrightarrow\sqrt{\left(x-1\right)+4\sqrt{x-1}+4}-\sqrt{4\left(x-1\right)+4\sqrt{x-1}+1}=1\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}+2\right)^2}-\sqrt{\left(2\sqrt{x-1}+1\right)^2}=1\)
\(\Leftrightarrow\left(\sqrt{x-1}+2\right)-\left(2\sqrt{x-1}+1\right)=1\)
\(\Leftrightarrow\sqrt{x-1}=0\)
\(\Leftrightarrow x=1\)(thõa mãn điều kiện)
Ta có : \(\sqrt{x+4\sqrt{x-1}+3}-\sqrt{4x+4\sqrt{x-1}-3}=1\) ( ĐK : \(x\ge1\) )
\(\Leftrightarrow\sqrt{\left(x-1\right)+4\sqrt{x-1}+4}-\sqrt{4.\left(x-1\right)+4.\sqrt{x-1}+1}=1\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}+2\right)^2}-\sqrt{\left(2\sqrt{x-1}+1\right)^2}=1\)
\(\Leftrightarrow\left|\sqrt{x-1}+2\right|-\left|2\sqrt{x-1}+1\right|=1\)
\(\Leftrightarrow\sqrt{x-1}+2-2\sqrt{x-1}-1=1\)
\(\Leftrightarrow\sqrt{x-1}=0\)
\(\Leftrightarrow x-1=0\)
\(\Leftrightarrow x=1\) ( Thỏa mãn )
\(x^2-x+8=4\sqrt{x+3}\)đk : x >= -3
\(\Leftrightarrow x\left(x-1\right)+8-4\sqrt{x+3}=0\)
Đặt \(\sqrt{x+3}=t;\Rightarrow x+3=t^2\Leftrightarrow x=t^2-3;x-1=t^2-4\)
khi đó : \(\left(t^2-3\right)\left(t^2-4\right)+8-4t=0\)
\(\Leftrightarrow t^4-7t^2+20-4t=0\)
\(\Leftrightarrow\left(t-2\right)\left(t^3+2t^2-3t-10\right)=0\)
\(\Leftrightarrow t=2;t=\frac{-4+2i}{2}\left(loại\right);\frac{-4-2i}{2}\left(loại\right)\)
Theo cách đặt \(\sqrt{x+3}=2\Leftrightarrow x+3=4\Leftrightarrow x=1\)
xin vui lòng giúp em, em rất rất gấp!!