Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
b)
(sin2x + cos2x)cosx + 2cos2x - sinx = 0
⇔ cos2x (cosx + 2) + sinx (2cos2 x – 1) = 0
⇔ cos2x (cosx + 2) + sinx.cos2x = 0
⇔ cos2x (cosx + sinx + 2) = 0
⇔ cos2x = 0
⇔ 2x =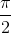 
+ kπ ⇔ x = 
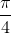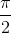+ k
(k ∈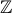 
)
c)
Đáp án:
x=π6π6+ k2ππ
và x= 5π65π6+k2ππ (k∈Z)
Lời giải:
sin2x-cos2x+3sinx-cosx-1=0
⇔ 2sinxcosx-(1-2sin²x) +3sinx-cosx-1=0
⇔ 2sin²x+2sinxcosx+3sinx-cosx-2=0
⇔ (2sin²x+3sinx-2)+ cosx(2sinx-1)=0
⇔ (2sinx-1)(sinx+2)+cosx(2sinx-1)=0
⇔ (2sinx-1)(sinx+cosx+2)=0
⇔ sinx=1212
⇔ x=π6π6+ k2ππ
hoặc x= 5π65π6+k2ππ (k∈Z)
(sinx+cosx+2)=0 (vô nghiệm do sinx+cosx+2=√22sin(x+π4π4)+2>0)
ĐK: \(x\ne k\pi\)
\(\dfrac{1+sin2x+cos2x}{1+cot^2x}=sinx.\left(sin2x+2sin^2x\right)\)
\(\Leftrightarrow\dfrac{1+sin2x+cos2x}{\dfrac{cos^2x+sin^2x}{sin^2x}}=sinx.\left(2sinx.cosx+2sin^2x\right)\)
\(\Leftrightarrow\dfrac{1+sin2x+cos2x}{\dfrac{1}{sin^2x}}=2sin^2x.\left(cosx+sinx\right)\)
\(\Leftrightarrow1+sin2x+cos2x=2cosx+2sinx\)
\(\Leftrightarrow1+2sinx.cosx+2cos^2x-1=2cosx+2sinx\)
\(\Leftrightarrow\left(cosx-1\right).\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left(cosx-1\right).sin\left(x+\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\sin\left(x+\dfrac{\pi}{4}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x+\dfrac{\pi}{4}=k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=-\dfrac{\pi}{4}+k\pi\end{matrix}\right.\)
a) \(\sin x = \frac{{\sqrt 3 }}{2}\;\; \Leftrightarrow \sin x = \sin \frac{\pi }{3}\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{3} + k2\pi }\\{x = \pi - \frac{\pi }{3} + k2\pi }\end{array}} \right.\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{3} + k2\pi }\\{x = \frac{{2\pi }}{3} + k2\pi \;}\end{array}\;} \right.\left( {k \in \mathbb{Z}} \right)\)
b) \(2\cos x = - \sqrt 2 \;\; \Leftrightarrow \cos x = - \frac{{\sqrt 2 }}{2}\;\;\; \Leftrightarrow \cos x = \cos \frac{{3\pi }}{4}\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{{3\pi }}{4} + k2\pi }\\{x = - \frac{{3\pi }}{4} + k2\pi }\end{array}\;\;\left( {k \in \mathbb{Z}} \right)} \right.\)
c) \(\sqrt 3 \;\left( {\tan \frac{x}{2} + {{15}^0}} \right) = 1\;\;\; \Leftrightarrow \tan \left( {\frac{x}{2} + \frac{\pi }{{12}}} \right) = \frac{1}{{\sqrt 3 }}\;\; \Leftrightarrow \tan \left( {\frac{x}{2} + \frac{\pi }{{12}}} \right) = \tan \frac{\pi }{6}\)
\( \Leftrightarrow \frac{x}{2} + \frac{\pi }{{12}} = \frac{\pi }{6} + k\pi \;\;\;\; \Leftrightarrow \frac{x}{2} = \frac{\pi }{{12}} + k\pi \;\;\; \Leftrightarrow x = \frac{\pi }{6} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
d) \(\cot \left( {2x - 1} \right) = \cot \frac{\pi }{5}\;\;\;\; \Leftrightarrow 2x - 1 = \frac{\pi }{5} + k\pi \;\;\;\; \Leftrightarrow 2x = \frac{\pi }{5} + 1 + k\pi \;\; \Leftrightarrow x = \frac{\pi }{{10}} + \frac{1}{2} + \frac{{k\pi }}{2}\;\;\left( {k \in \mathbb{Z}} \right)\)
ĐKXĐ: \(\left\{{}\begin{matrix}sinx\ne0\\cos3x+cosx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}sinx\ne0\\2cos2x.cosx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\cos2x\ne0\end{matrix}\right.\)
Phương trình tương đương:
\(\left(sin3x-sinx\right)\left(\frac{cos^2x}{sin^2x}-1\right)=0\)
\(\Leftrightarrow2cos2x.sinx.\left(cos^2x-sin^2x\right)=0\)
\(\Leftrightarrow2cos^22x.sinx=0\)
Phương trình vô nghiệm
c.
\(\Leftrightarrow cos\left(x+12^0\right)+cos\left(90^0-78^0+x\right)=1\)
\(\Leftrightarrow2cos\left(x+12^0\right)=1\)
\(\Leftrightarrow cos\left(x+12^0\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+12^0=60^0+k360^0\\x+12^0=-60^0+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=48^0+k360^0\\x=-72^0+k360^0\end{matrix}\right.\)
2.
Do \(-1\le sin\left(3x-27^0\right)\le1\) nên pt có nghiệm khi:
\(\left\{{}\begin{matrix}2m^2+m\ge-1\\2m^2+m\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2m^2+m+1\ge0\left(luôn-đúng\right)\\2m^2+m-1\le0\end{matrix}\right.\)
\(\Rightarrow-1\le m\le\dfrac{1}{2}\)
a.
\(\Rightarrow\left[{}\begin{matrix}x+15^0=arccos\left(\dfrac{2}{5}\right)+k360^0\\x+15^0=-arccos\left(\dfrac{2}{5}\right)+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-15^0+arccos\left(\dfrac{2}{5}\right)+k360^0\\x=-15^0-arccos\left(\dfrac{2}{5}\right)+k360^0\end{matrix}\right.\)
b.
\(2x-10^0=arccot\left(4\right)+k180^0\)
\(\Rightarrow x=5^0+\dfrac{1}{2}arccot\left(4\right)+k90^0\)
ĐKXĐ: \(sinx\ne0\)
\(\Leftrightarrow cot^2x=\left|\frac{1-\left|sinx\right|}{1-\left|cosx\right|}\right|\Leftrightarrow cot^2x=\frac{1-\left|sinx\right|}{1-\left|cosx\right|}\)
Đặt \(\left\{{}\begin{matrix}\left|sinx\right|=a\Rightarrow0< a\le1\\\left|cosx\right|=b\Rightarrow0\le b< 1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a^2+b^2=1\\\frac{b^2}{a^2}=\frac{1-a}{1-b}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a^2+b^2=1\\\frac{b^2}{1-b^2}=\frac{1-a}{1-b}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2+b^2=1\\\frac{b^2}{\left(1-b\right)\left(1+b\right)}=\frac{\left(1-a\right)\left(1+b\right)}{\left(1-b\right)\left(1+b\right)}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a^2+b^2=1\\1-a^2=\left(1-a\right)\left(1-b\right)\end{matrix}\right.\)
\(\Rightarrow\left(1-a\right)\left(1+a\right)=\left(1-a\right)\left(1-b\right)\)
\(\Rightarrow\left[{}\begin{matrix}a=1\\1+a=1-b\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}a=1\\a+b=0\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow\left|sinx\right|=1\Leftrightarrow sin^2x=1\Leftrightarrow cosx=0\Leftrightarrow x=...\)