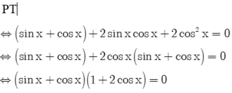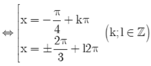Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) <=> 4sinxcosx -(2cos2x-1)=7sinx+2cosx-4
<=> 2cos2x+(2-4sinx)cosx+7sinx-5=0
- sinx=1 => 2cos2x-2cosx+2=0
pt trên vn
b) <=> 2sinxcosx-1+2sin2x+3sinx-cosx-1=0
<=> cos(2sinx-1)+2sin2x+3sinx-2=0
<=> cosx(2sinx-1)+(2sinx-1)(sinx+2)=0
<=> (2sinx-1)(cosx+sinx+2)=0
<=> sinx=1/2 hoặc cosx+sinx=-2(vn)
<=> x= \(\frac{\pi}{6}+k2\pi\) hoặc \(x=\frac{5\pi}{6}+k2\pi\left(k\in Z\right)\)

1.
\(\Leftrightarrow sin^2x\left(sinx+1\right)-2\left(1-cosx\right)=0\)
\(\Leftrightarrow\left(1-cos^2x\right)\left(sinx+1\right)-2\left(1-cosx\right)=0\)
\(\Leftrightarrow\left(1-cosx\right)\left(1+cosx\right)\left(sinx+1\right)-2\left(1-cosx\right)=0\)
\(\Leftrightarrow\left(1-cosx\right)\left(sinx+cosx+sinx.cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\Leftrightarrow...\\sinx+cosx+sinx.cosx-1=0\left(1\right)\end{matrix}\right.\)
Xét (1):
Đặt \(sinx+cosx=t\Rightarrow\left[{}\begin{matrix}\left|t\right|\le\sqrt{2}\\sinx.cosx=\frac{t^2-1}{2}\end{matrix}\right.\)
\(\Leftrightarrow t+\frac{t^2-1}{2}-1=0\)
\(\Leftrightarrow t^2+2t-3=0\Rightarrow\left[{}\begin{matrix}t=1\\t=-3\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow sin\left(x+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow...\)
2.
\(\Leftrightarrow\sqrt{3}sinx.cosx+\sqrt{2}cos^2x+\sqrt{6}cosx=0\)
\(\Leftrightarrow cosx\left(\sqrt{3}sinx+\sqrt{2}cosx+\sqrt{6}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\Leftrightarrow...\\\sqrt{3}sinx+\sqrt{2}cosx=-\sqrt{6}\left(1\right)\end{matrix}\right.\)
Xét (1):
Do \(\sqrt{3}^2+\sqrt{2}^2< \left(-\sqrt{6}\right)^2\) nên (1) vô nghiệm

<=> (2sinxcosx-cosx)+5sinx-2-cos2x=0
<=> cosx(2sinx-1)+2\(sin^2x\)+5sinx-3=0
<=> cosx(2sinx-1) +(2sinx-1)(sinx+3)
<=> (2sinx-1)(cosx+sinx+3)=0
<=>\(\begin{cases}sinx=\frac{1}{2}\\cosx+sinx+3=0\end{cases}\)
+) sinx=1/2
<=> \(x=\frac{\pi}{2}+k2\pi\) với k thuộc Z
+) cosx+sinx+3= <=>\(\sqrt{2}sin\left(x+\frac{\pi}{4}\right)\)=-3
<=> \(sin\left(x+\frac{\pi}{4}\right)\)=\(\frac{-\sqrt{3}}{2}\)
<=>\(sin\left(x+\frac{\pi}{4}\right)=sin\frac{-\pi}{3}\)
<=> \(\left[\begin{array}{nghiempt}x=\frac{-\pi}{3}+k2\pi\\x=\frac{4\pi}{3}+k2\pi\end{array}\right.\)với k thuộc Z
vậy pht có 3 nghiệm:..

\(sin2x-cos2x+3sinx-cosx-1=0\)
\(\Leftrightarrow2sinxcosx-\left(1-2sin^2x\right)+3sinx-cosx-1=0\)
\(\Leftrightarrow2sinxcosx-1+2sin^2x+3sinx-cosx-1=0\)
\(\Leftrightarrow2sin^2x+3sinx-2+cosx\left(2sinx-1\right)=0\)
\(\Leftrightarrow2\left(sinx-\dfrac{1}{2}\right)\left(sinx+2\right)+cosx\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx+2\right)+cosx\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx+2+cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2sinx-1=0\\sinx+cosx+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\sinx+cosx=-2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}sinx=sin\dfrac{\pi}{6}\\\sqrt[]{2}\left(sinx.\dfrac{1}{\sqrt[]{2}}+cosx.\dfrac{1}{\sqrt[]{2}}\right)=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\\\sqrt[]{2}sin\left(x+\dfrac{\pi}{4}\right)=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\\sin\left(x+\dfrac{\pi}{4}\right)=-\sqrt[]{2}\left(vô.lý\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\) \(\left(k\in Z\right)\)


ĐK: \(x\ne\dfrac{\pi}{4}+k\pi;x\ne\dfrac{k\pi}{2}\)
\(\dfrac{2sin^2x+cos4x-cos2x}{\left(sinx-cosx\right)sin2x}=0\)
\(\Leftrightarrow2sin^2x+cos4x-cos2x=0\)
\(\Leftrightarrow2sin^2x-1+cos4x-cos2x+1=0\)
\(\Leftrightarrow2cos^22x-2cos2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cos2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}+k\pi\\2x=k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x=k\pi\end{matrix}\right.\)
Đối chiếu điều kiện ta được \(x=-\dfrac{\pi}{4}+k\pi\)

`cos 2x+\sqrt{3}sin 2x+\sqrt{3}sin x-cos x=4`
`<=>1/2 cos 2x+\sqrt{3}/2 sin 2x+\sqrt{3}/2 sin x-1/2 cos x=2`
`<=>sin(\pi/6 +2x)+sin(x-\pi/6)=2`
Vì `-1 <= sin (\pi/6 +2x) <= 1`
`-1 <= sin (x-\pi/6) <= 1`
Dấu "`=`" xảy ra `<=>{(sin(\pi/6+2x)=1),(sin(x-\pi/6)=1):}`
`<=>{(\pi/6+2x=\pi/2+k2\pi),(x-\pi/6=\pi/2+k2\pi):}`
`<=>{(x=\pi/6+k\pi),(x=[2\pi]/3+k2\pi):}` `(k in ZZ)`

Pt <=> 2sin\(\dfrac{3x}{2}\).cos\(\dfrac{x}{2}\) = 2cos\(\dfrac{3x}{2}\).cos\(\dfrac{x}{2}\)
⇔ cos\(\dfrac{x}{2}\) . \(\left(sin\dfrac{3x}{2}-cos\dfrac{3x}{2}\right)\) = 0
⇔ \(\sqrt{2}sin\left(\dfrac{3x}{2}-\dfrac{\pi}{4}\right).cos\dfrac{x}{2}=0\)
⇔