
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)=1-sinx.cosx\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(1-sinx.cosx\right)=1-sinx.cosx\)
\(\Leftrightarrow\left(1-sinx.cosx\right)\left(sinx+cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx.cosx=1\\sinx+cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=2\left(vn\right)\\\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\end{matrix}\right.\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\pi-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
2.
\(\left|cosx-sinx\right|+2sin2x=1\)
\(\Leftrightarrow\left|cosx-sinx\right|-1+2sin2x=0\)
\(\Leftrightarrow\left|cosx-sinx\right|-\left(cosx-sinx\right)^2=0\)
\(\Leftrightarrow\left|cosx-sinx\right|\left(1-\left|cosx-sinx\right|\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)=0\\\left|cosx-sinx\right|=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=k\pi\\cos^2x+sin^2x-2sinx.cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\1-sin2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\sin2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{k\pi}{2}\end{matrix}\right.\)

a, (sinx + cosx)(1 - sinx . cosx) = (cosx - sinx)(cosx + sinx)
⇔ \(\left[{}\begin{matrix}sinx+cosx=0\\cosx-sinx=1-sinx.cosx\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}sinx+cosx=0\\cosx+sinx.cosx-1-sinx=0\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}sinx+cosx=0\\\left(cosx-1\right)\left(sinx+1\right)=0\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}sin\left(x+\dfrac{\pi}{4}\right)=0\\cosx=1\\sinx=-1\end{matrix}\right.\)
b, (sinx + cosx)(1 - sinx . cosx) = 2sin2x + sinx + cosx
⇔ (sinx + cosx)(1 - sinx.cosx - 1) = 2sin2x
⇔ (sinx + cosx).(- sinx . cosx) = 2sin2x
⇔ 4sin2x + (sinx + cosx) . sin2x = 0
⇔ \(\left[{}\begin{matrix}sin2x=0\\\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+4=0\end{matrix}\right.\)
⇔ sin2x = 0
c, 2cos3x = sin3x
⇔ 2cos3x = 3sinx - 4sin3x
⇔ 4sin3x + 2cos3x - 3sinx(sin2x + cos2x) = 0
⇔ sin3x + 2cos3x - 3sinx.cos2x = 0
Xét cosx = 0 : thay vào phương trình ta được sinx = 0. Không có cung x nào có cả cos và sin = 0 nên cosx = 0 không thỏa mãn phương trình
Xét cosx ≠ 0 chia cả 2 vế cho cos3x ta được :
tan3x + 2 - 3tanx = 0
⇔ \(\left[{}\begin{matrix}tanx=1\\tanx=-2\end{matrix}\right.\)
d, cos2x - \(\sqrt{3}sin2x\) = 1 + sin2x
⇔ cos2x - sin2x - \(\sqrt{3}sin2x\) = 1
⇔ cos2x - \(\sqrt{3}sin2x\) = 1
⇔ \(2cos\left(2x+\dfrac{\pi}{3}\right)=1\)
⇔ \(cos\left(2x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}=cos\dfrac{\pi}{3}\)
e, cos3x + sin3x = 2cos5x + 2sin5x
⇔ cos3x (1 - 2cos2x) + sin3x (1 - 2sin2x) = 0
⇔ cos3x . (- cos2x) + sin3x . cos2x = 0
⇔ \(\left[{}\begin{matrix}sin^3x=cos^3x\\cos2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}sinx=cosx\\cos2x=0\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)=0\\cos2x=0\end{matrix}\right.\)

c/
\(\Leftrightarrow1-cos^2\frac{x}{2}-2cos\frac{x}{2}+2=0\)
\(\Leftrightarrow cos^2\frac{x}{2}+2cos\frac{x}{2}-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\frac{x}{2}=1\\cos\frac{x}{2}=-3< -1\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow\frac{x}{2}=k2\pi\)
\(\Leftrightarrow x=k4\pi\)
d/ ĐKXĐ: ...
\(\Leftrightarrow tanx-\frac{2}{tanx}+1=0\)
\(\Leftrightarrow tan^2x+tanx-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tanx=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=arctan\left(-2\right)+k\pi\end{matrix}\right.\)
a/
\(\Leftrightarrow\left(cosx-1\right)\left(2cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pm\frac{\pi}{3}+k2\pi\end{matrix}\right.\)
b \(\Leftrightarrow2sin2x+2\sqrt{2}sin2x.cos2x=0\)
\(\Leftrightarrow2sin2x\left(1+\sqrt{2}cos2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\cos2x=-\frac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=k\pi\\2x=\pm\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{2}\\x=\pm\frac{3\pi}{8}+k\pi\end{matrix}\right.\)

a.
\(y=2\left(1-cos2x\right)-\dfrac{5}{2}sin2x+\dfrac{1}{2}+\dfrac{1}{2}cos2x+10\)
\(=-\dfrac{1}{2}\left(5sin2x+3cos2x\right)+\dfrac{25}{2}\)
\(=-\dfrac{\sqrt{34}}{2}\left(\dfrac{5}{\sqrt{34}}sin2x+\dfrac{3}{\sqrt{34}}cos2x\right)+\dfrac{25}{2}\)
Đặt \(\dfrac{5}{\sqrt{34}}=cosa\)
\(\Rightarrow y=-\dfrac{\sqrt{34}}{2}\left(sin2x.cosa+cos2x.sina\right)+\dfrac{25}{2}\)
\(=-\dfrac{\sqrt{34}}{2}sin\left(2x+a\right)+\dfrac{25}{2}\)
Do \(-1\le sin\left(2x+a\right)\le1\)
\(\Rightarrow\dfrac{25-\sqrt{34}}{2}\le y\le\dfrac{25+\sqrt{34}}{2}\)
b.
\(y=\dfrac{sin^2x-2sin2x+1}{3+sin^2x+2cos^2x}=\dfrac{2sin^2x-4sin2x+2}{6+2\left(sin^2x+cos^2x\right)+2cos^2x}\)
\(=\dfrac{1-cos2x-4sin2x+2}{8+1+cos2x}=\dfrac{3-4sin2x-cos2x}{9+cos2x}\)
\(\Rightarrow9y+y.cos2x=3-4sin2x-cos2x\)
\(\Rightarrow4sin2x+\left(y+1\right)cos2x=3-9y\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(4^2+\left(y+1\right)^2\ge\left(3-9y\right)^2\)
\(\Leftrightarrow80y^2-56y-8\le0\)
\(\Rightarrow\dfrac{7-\sqrt{89}}{20}\le y\le\dfrac{7+\sqrt{89}}{20}\)

\(\sqrt{3}cos\left(x+\dfrac{\pi}{2}\right)+sin\left(x-\dfrac{\pi}{2}\right)=2sin2x\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sin\left(\dfrac{\pi}{2}-x-\dfrac{\pi}{2}\right)-\dfrac{1}{2}cos\left(\dfrac{\pi}{2}-\dfrac{\pi}{2}+x\right)=sin2x\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sinx+\dfrac{1}{2}cosx+sin2x=0\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{6}\right)+sin2x=0\)
\(\Leftrightarrow2sin\left(\dfrac{3x}{2}+\dfrac{\pi}{12}\right).cos\left(\dfrac{\pi}{12}-\dfrac{x}{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(\dfrac{3x}{2}+\dfrac{\pi}{12}\right)=0\\cos\left(\dfrac{\pi}{12}-\dfrac{x}{2}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{3x}{2}+\dfrac{\pi}{12}=k\pi\\\dfrac{\pi}{12}-\dfrac{x}{2}=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{18}+\dfrac{k2\pi}{3}\\x=-\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)

2cos2x – 3cosx + 1 = 0 (Phương trình bậc hai với ẩn cos x).
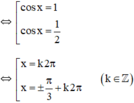
Vậy phương trình có tập nghiệm
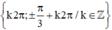
![Giải phương trình lượng giác: a) 1 + tanx = 2√2.sinx; b) [sin^2x(sinx - 1)] : (sinx + cosx) = 4cos^2(x/2) - Toán học Lớp 11 - Bài tập Toán học Lớp 11 - Giải bài tập Toán học Lớp 11 Giải phương trình lượng giác,1 + tanx = 2căn2.sinx,[sin^2x(sinx - 1)] : (sinx + cosx) = 4cos^2(x/2),Toán học Lớp 11,bài tập Toán học Lớp 11,giải bài tập Toán học Lớp 11,Toán học,Lớp 11](https://lazi.vn/uploads/edu/answer/1502109525_502.jpg)
![Giải phương trình lượng giác: a) 1 + tanx = 2√2.sinx; b) [sin^2x(sinx - 1)] : (sinx + cosx) = 4cos^2(x/2) - Toán học Lớp 11 - Bài tập Toán học Lớp 11 - Giải bài tập Toán học Lớp 11 Giải phương trình lượng giác,1 + tanx = 2căn2.sinx,[sin^2x(sinx - 1)] : (sinx + cosx) = 4cos^2(x/2),Toán học Lớp 11,bài tập Toán học Lớp 11,giải bài tập Toán học Lớp 11,Toán học,Lớp 11](https://lazi.vn/uploads/edu/answer/1502117801_501.jpg)
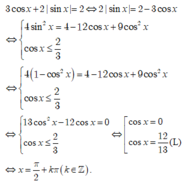
\(sin^3x+2sinx+3cosx=0\)
\(\Leftrightarrow sin^3x-sinx+3sinx+3cosx=0\)
\(\Leftrightarrow sinx\left(sin^2x-1\right)+3\left(sinx+cosx\right)=0\)
\(\Leftrightarrow-sinx.cosx+3\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\dfrac{1-\left(sinx+cosx\right)^2}{2}+3\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)^2-6\left(sinx+cosx\right)-1=0\)
\(\Leftrightarrow\left(sinx+cosx\right)^2-6\left(sinx+cosx\right)-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=3+\sqrt{10}\\sinx+cosx=3-\sqrt{10}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{3+\sqrt{10}}{\sqrt{2}}\left(l\right)\\sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{3-\sqrt{10}}{\sqrt{2}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=arcsin\left(\dfrac{3-\sqrt{10}}{\sqrt{2}}\right)+k2\pi\\x+\dfrac{\pi}{4}=\pi-arcsin\left(\dfrac{3-\sqrt{10}}{\sqrt{2}}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+arcsin\left(\dfrac{3-\sqrt{10}}{\sqrt{2}}\right)+k2\pi\\x=\dfrac{3\pi}{4}-arcsin\left(\dfrac{3-\sqrt{10}}{\sqrt{2}}\right)+k2\pi\end{matrix}\right.\)