
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow\frac{3^{\sin^2x}+3}{3^{\sin^2x}}-4=2^{2.\frac{x}{2}}+2^{2.\frac{-x}{2}}-2\)
\(\Leftrightarrow\frac{\left(3^{\sin^2x}-1\right)\left(3^{\sin^2x}-3\right)}{3^{\sin^2x}}=\left(2^{\frac{x}{2}}-2^{\frac{-x}{2}}\right)^2\)
Vì 0 \(\le\sin^2x\)\(\le1\) nên 1 \(\le3\sin^2x\)\(\le3\) . Suy ra Vế trái \(\le0\)\(\le\) vế phải và phương trình tương đương với hệ :
\(\begin{cases}\left(3^{\sin^2x}-1\right)\left(3^{\sin^2x}-3\right)=0\\2^{\frac{x}{2}}-2^{\frac{-x}{2}}=0\end{cases}\)
Từ phương trình thứ 2, dễ dàng suy ra x=0 (thỏa mãn). Vậy x=0 là nghiệm duy nhất của phương trình đã cho.

Chọn C
Ta có: ![]() nên (1) và (2) có nghiệm.
nên (1) và (2) có nghiệm.
Cách 1:
Xét: ![]()
![]() nên (3) vô nghiệm.
nên (3) vô nghiệm.
Cách 2:
Điều kiện có nghiệm của phương trình: sin x + cos x = 2 là: 
(vô lý) nên (3) vô nghiệm.
Cách 3:
Vì 

nên (3) vô nghiệm.




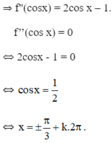
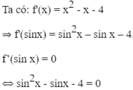
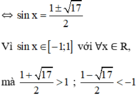
\(4\left(\sin^4x+\cos^4x\right)+\sqrt{3}\sin4x=2\)
<=> \(4\left[\left(\sin^2x+\cos^2x\right)^2-2\sin^2x.\cos^2x\right]+\sqrt{3}\sin4x=2\)
<=> \(4\left(1-\frac{1}{2}\sin^22x\right)+\sqrt{3}\sin4x=2\)
<=> \(4-2\sin^22x+\sqrt{3}\sin4x=2\)
<=> \(-2\sin^22x+\sqrt{3}\sin4x=-2\)
<=> \(\cos4x-1+\sqrt{3}\sin4x=-2\)
<=> \(\cos4x+\sqrt{3}\sin4x=-1\)
<=> \(\frac{1}{2}\cos4x+\frac{\sqrt{3}}{2}\sin4x=-\frac{1}{2}\)
<=> \(\cos\frac{\pi}{3}.\cos4x+\sin\frac{\pi}{3}.\sin4x=\cos\frac{2\pi}{3}\)
<=> \(\cos\left(4x-\text{}\text{}\frac{\pi}{3}\right)=\cos\frac{2\pi}{3}\)
Phương trình lượng giác cơ bản. Em làm tiếp nhé!