
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


6x^3 + x + 4 = 11x^2
<=>6x3-11x2+x+4=0
<=>6x3+3x2-14x2-7x+8x+4=0
<=>3x2(2x+1)-7x(2x+1)+4(2x+1)=0
<=>(2x+1)(3x2-7x+4)=0
<=>(2x+1)(3x2-3x-4x+4)=0
<=>(2x+1)(3x-4)(x-1)=0
<=>2x+1=0 hoặc 3x-4=0 hoặc x-1=0
<=>x\(\in\){-1/2;1;4/3}
b)x^6 - 14x^4 + 49x^2 = 36
<=>x6-14x4+49x2-36=0
<=>x6-x4-13x4+13x2+36x2-36=0
<=>x4(x2-1)-13x2(x2-1)+36(x2-1)=0
<=>(x2-1)(x4-13x2+36)=0
<=>(x+1)(x-1)(x4-9x2-4x2+36)=0
<=>(x+1)(x-1)[x2(x2-9)-4(x2-9)]=0
<=>(x-1)(x+1)(x2
-9)(x2-4)=0
<=>(x-1)(x+1)(x+3)(x-3)(x+2)(x-2)=0
<=>x\(\in\){-3;-2;-1;1;2;3}
p/s: kham khảo

6x^3 + x + 4 = 11x^2
<=>6x3-11x2+x+4=0
<=>6x3+3x2-14x2-7x+8x+4=0
<=>3x2(2x+1)-7x(2x+1)+4(2x+1)=0
<=>(2x+1)(3x2-7x+4)=0
<=>(2x+1)(3x2-3x-4x+4)=0
<=>(2x+1)(3x-4)(x-1)=0
<=>2x+1=0 hoặc 3x-4=0 hoặc x-1=0
<=>x\(\in\){-1/2;1;4/3}
b)x^6 - 14x^4 + 49x^2 = 36
<=>x6-14x4+49x2-36=0
<=>x6-x4-13x4+13x2+36x2-36=0
<=>x4(x2-1)-13x2(x2-1)+36(x2-1)=0
<=>(x2-1)(x4-13x2+36)=0
<=>(x+1)(x-1)(x4-9x2-4x2+36)=0
<=>(x+1)(x-1)[x2(x2-9)-4(x2-9)]=0
<=>(x-1)(x+1)(x2-9)(x2-4)=0
<=>(x-1)(x+1)(x+3)(x-3)(x+2)(x-2)=0
<=>x\(\in\){-3;-2;-1;1;2;3}
phù.mệt


a, \(12-2\left(1-x\right)^2=\left(3x-2\right)\left(2x-3\right)\)
\(< =>12-2\left(1-2x+x^2\right)=6x^2-9x-4x+6\)
\(< =>12-2+4x-2x^2=6x^2-13x+6\)
\(< =>10+4x-2x^2-6x^2+13x-6=0\)
\(< =>-8x^2+17x+4=0< =>\orbr{\begin{cases}x=\frac{17-\sqrt{417}}{16}\\x=\frac{17+\sqrt{417}}{16}\end{cases}}\)
b, \(10x+3-5x=4x+12< =>5x+3-4x-12=0\)
\(< =>x-9=0< =>x=9\)
c, \(11x+42-2x=100-9x-22< =>9x+42-100+9x+22=0\)
\(< =>18x+64-100=0< =>18x-36=0< =>x=\frac{36}{18}=2\)
d, \(2x-\left(3-5x\right)=4\left(x+3\right)< =>2x-3+5x=4x+12\)
\(< =>7x-3-4x-12=0< =>3x-15=0< =>x=\frac{15}{3}=5\)
e, \(2\left(x-3\right)+5x\left(x-1\right)=5x^2< =>2x-6+5x^2-5=5x^2\)
\(< =>2x-11+5x^2-5x^2=0< =>2x-11=0< =>x=\frac{11}{2}\)
f, \(-6\left(1,5-2x\right)=3\left(-15+2x\right)< =>-6\left(\frac{3}{2}-2x\right)=3\left(2x-15\right)\)
\(< =>-9+12x-6x+45=0< =>6x+36=0< =>x=-6\)
g, \(14x-\left(2x+7\right)=3x+12x-13< =>14x-2x-7=15x-13\)
\(< =>12x-7-15x+13=0< =>-3x+6=0< =>x=-2\)
h, \(\left(x-4\right)\left(x+4\right)-2\left(3x-2\right)=\left(x-4\right)^2\)
\(< =>x^2-16-6x+4=x^2-8x+16\)
\(< =>x^2-6x-12-x^2+8x-16=0\)
\(< =>2x-28=0< =>x=\frac{28}{2}=14\)
q, \(4\left(x-2\right)-\left(x-3\right)\left(2x-5\right)=?\)thiếu đề

a) (2x – 1)(4x2 + 2x + 1) – 4x(2x2 – 3) = 23
⇔ 8x3 – 1 – 8x3 + 12x = 23
⇔ 12x = 24 ⇔ x = 2.
Tập nghiệm của phương trình: S = {2}
b) ĐKXĐ : x + 1 ≠ 0 và x – 2 ≠ 0 (vì vậy x2 – x – 2 = (x + 1)(x – 2) ≠ 0)
⇔ x ≠ -1 và x ≠ 2
Quy đồng mẫu thức hai vế :
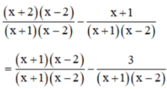
Khử mẫu, ta được : x2 – 4 – x – 1 = x2 – x – 2 – 3 ⇔ 0x = 0
Phương trình này luôn nghiệm đúng với mọi x ≠ -1 và x ≠ 2.

a) x(x+2)=x(x+3)
<-> x(x+2)-x(x+3)=0
<-> x(x+2-x-3)=0
<-> x(-1)=0
<-> x=0
Vậy x=0 là nghiệm của phương trình
a, x^2 + 2x - x^2 - 3x = 0
<=> -x = 0
<=> x = 0
b, 11x + 42 - 2x - 100 + 9x + 22 = 0
<=> 18x - 36 = 0
<=> 18x = 36
<=> x = 2

a) 8( 3x - 2 ) - 14x = 2( 4 – 7x ) + 15x
⇔ 24x – 16 -14x = 8 – 14x + 15x
⇔ 10x -16 = 8 + x
⇔ 9x = 24
⇔ x = 24/9
b) ( 3x – 1 )( x – 3 ) – 9 + x2 = 0
⇔ (3x -1)( x – 3) + (x - 3)( x + 3) = 0
⇔ (x - 3)(3x - 1 + x - 3) = 0
⇔ (x - 3)(4x - 4) = 0
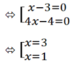
c) |x - 2| = 2x - 3
TH1: x - 2 ≥ 0 ⇔ x ≥ 2
Khi đó: x - 2 = 2x – 3
⇔ 2x – x = -2 + 3
⇔ x = 1 (không TM điều kiện x ≥ 2)
TH2: x – 2 < 0 ⇔ x < 2
Khi đó: x-2 = -(2x – 3)
⇔ x – 2 = -2x + 3
⇔ 3x = 5
⇔ x = 5/3 ( TM điều kiện x < 2)
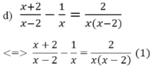
MTC: x(x-2)
ĐKXĐ: x ≠ 0;x ≠ 2

Đối chiếu với ĐKXĐ thì pt có nghiệm x = - 1

c) \(\dfrac{x}{x-2}+\dfrac{x}{x+2}=\dfrac{4x}{x^2-4}.ĐKXĐ:x\ne2;-2\)
<=>\(\dfrac{x\left(x+2\right)}{x^2-4}+\dfrac{x\left(x-2\right)}{x^2-4}=\dfrac{4x}{x^2-4}\)
<=>x2+2x+x2-2x=4x
<=>2x2-4x=0
<=>2x(x-2)=0
<=>\(\left[{}\begin{matrix}2x=0< =>x=0\\x-2=0< =>x=2\left(loại\right)\end{matrix}\right.\)
Vậy pt trên có nghiệm là S={0}
d) 11x-9=5x+3
<=>11x-5x=9+3
<=>6x=12
<=>x=2
Vậy pt trên có nghiệm là S={2}
e) (2x+3)(3x-4) =0
<=> \(\left[{}\begin{matrix}2x+3=0< =>x=\dfrac{-3}{2}\\3x-4=0< =>x=\dfrac{4}{3}\end{matrix}\right.\)
Vậy pt trên có tập nghiệm là S={\(\dfrac{-3}{2};\dfrac{4}{3}\)}
a) 5x+9 =2x
<=> 5x-2x=9
<=> 3x=9
<=> x=3
Vậy pt trên có nghiệm là S={3}
b) (x+1)(4x-3)=(2x+5)(x+1)
<=> (x+1)(4x-3)-(2x+5)(x+1)=0
<=>(x+1)(2x-8)=0
<=>\(\left[{}\begin{matrix}x+1=0< =>x=-1\\2x-8=0< =>2x=8< =>x=4\end{matrix}\right.\)
Vậy pt trên có tập nghiệm là S={-1;4}