Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
Gọi M là trung điểm BC thì theo tính chất trọng tâm: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)\)
\(\Rightarrow\overrightarrow{AG}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\Rightarrow x+y=\dfrac{2}{3}\)
2.
\(CH=\dfrac{1}{2}BC=\dfrac{a}{2}\)
\(T=\left|\text{ }\overrightarrow{CA}-\overrightarrow{HC}\right|=\left|\overrightarrow{CA}+\overrightarrow{CH}\right|\)
\(\Rightarrow T^2=CA^2+CH^2+2\overrightarrow{CA}.\overrightarrow{CH}=a^2+\left(\dfrac{a}{2}\right)^2+2.a.\dfrac{a}{2}.cos60^0=\dfrac{7a^2}{4}\)
\(\Rightarrow T=\dfrac{a\sqrt{7}}{2}\)
3.
\(10< x< 100\Rightarrow10< 3k< 100\)
\(\Rightarrow\dfrac{10}{3}< k< \dfrac{100}{3}\Rightarrow4\le k\le33\)
\(\Rightarrow\sum x=3\left(4+5+...+33\right)=1665\)

mk bận đi ch nên chỉ tạm câu a nha
vẽ 3 đường trung tuyến AD ; BE ; CF
VT =
\(GA+GB+GC\) ( nhớ thêm dấu vec tơ nha )
\(=-\frac{2}{3}AD-\frac{2}{3}BE-\frac{2}{3}CF\)
\(=-\frac{2}{3}\cdot\frac{1}{2}\left(AB+BC\right)-\frac{2}{3}\cdot\frac{1}{2}\left(BA+BC\right)-\frac{2}{3}\cdot\frac{1}{2}\left(CA+CB\right)\) ( quy tắc hình bình hành )
\(=-\frac{1}{3}\left(AB+AC\right)-\frac{1}{3}\left(BA+BC\right)-\frac{1}{3}\left(CA+CB\right)\)
\(=-\frac{1}{3}AB-\frac{1}{3}AC-\frac{1}{3}BA-\frac{1}{3}BC-\frac{1}{3}CA-\frac{1}{3}CB\)
\(=0=VP\)
Cho tam giác ABC có trung tuyến BM và trọng tâm G . Phân tích vecto BG theo hai vecto BA và vecto BC

\(\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BM}=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BC}\)

* cái này là công thức rồi bn o cần chứng minh đâu
công thức : cho tam giác ABC ; nếu G là trọng tâm của tam giác ABC thì \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
Gọi M trung điểm BC
G đối xứng D qua M
=> tứ giác BGCD là hình bình hành
=> GD=2.GM (Hình bình hành có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
Mà AG = 2.GM ( \(\dfrac{AG}{GM}=\dfrac{2}{1},GA=\dfrac{2}{3}AM\) )
⇒ AG=GD
Mặt khác, G ϵ AD
⇒\(\overrightarrow{AG}=\overrightarrow{GD}\)
Ta có \(\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GD}\) (Quy tắc hình bình hành)
Nên \(\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GA}\) = \(\overrightarrow{GD}+\overrightarrow{GA}\)
Mà \(\overrightarrow{AG}=\overrightarrow{GD}\) (cmt)
⇒\(\overrightarrow{AG}+\overrightarrow{GA}=\overrightarrow{AG}-\overrightarrow{AG}=\overrightarrow{O}\)
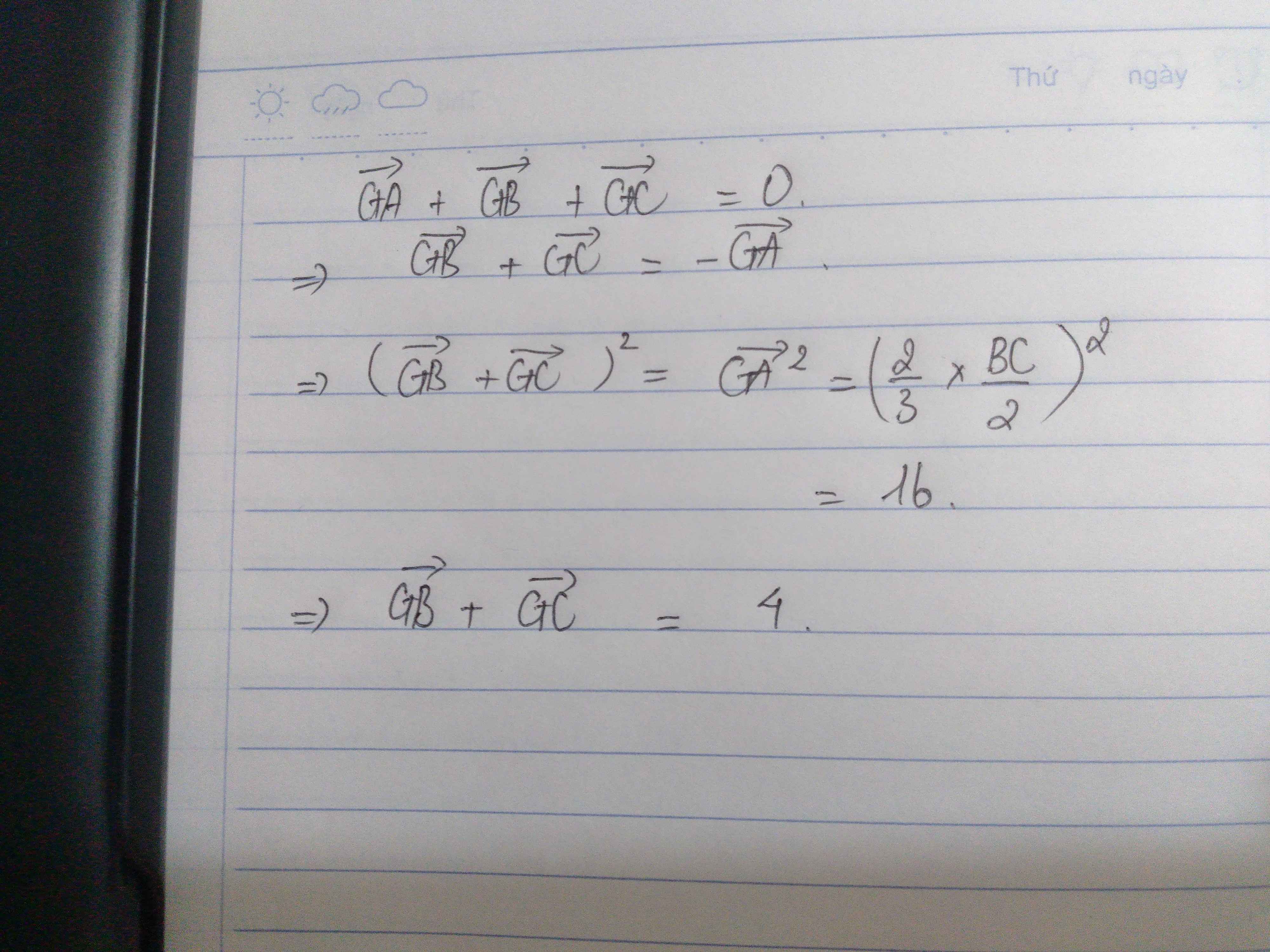
Do G là trọng tâm
\(\Rightarrow\overrightarrow{BG}=\dfrac{1}{3}\left(\overrightarrow{BA}+\overrightarrow{BC}\right)=-\dfrac{1}{3}AB+\dfrac{1}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
\(\Rightarrow T=-\dfrac{1}{3}\)
Để tính tổng T = x + y, ta cần tìm giá trị của x và y.
Theo định nghĩa, trọng tâm G của tam giác ABC là điểm giao của ba đường trung tuyến, tức là các đoạn thẳng nối mỗi đỉnh của tam giác với trung điểm của đoạn thẳng đối diện.
Trong bài toán này, ta biết rằng vecto BG có thể được biểu diễn bằng tổng của vecto AB và AC theo các hệ số x và y: BG = xAB + yAC.
Chúng ta cần tìm tổng x + y. Để làm điều này, ta có thể so sánh hệ số của vecto BG đã cho và biểu diễn vecto BG bằng các hệ số x và y:
Theo công thức trung điểm, ta có: BG = 1/2 BA + 1/2 BC.
So sánh với biểu diễn vecto BG đã cho: BG = xAB + yAC.
Áp dụng so sánh, ta có: 1/2 BA + 1/2 BC = xAB + yAC.
Vì BA + AC = BC (điều này có thể được chứng minh dựa trên tính chất của trọng tâm), ta có thể thay thế BC bằng BA + AC trong phương trình và thu gọn được: 1/2 BA + 1/2 (BA + AC) = xAB + yAC, 1/2 BA + 1/2 BA + 1/2 AC = xAB + yAC, BA + 1/2 AC = xAB + yAC.
So sánh hệ số của các vecto AB và AC, ta có hệ phương trình: x = 1, y = 1/2.
Vậy tổng T = x + y = 1 + 1/2 = 3/2.
Đáp án: T = 3/2.