Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có góc BDC là góc ngoài của tam giác vuông ADC nên góc BDC là góc tù
b) Ta có góc BDC là góc ngoài của tam giác ADC nên góc BDC = góc A + góc ACD
=> góc ACD = góc BDC - góc A = 105 độ - 90 độ = 15 độ
mà CD là tia phân giác của góc ACB nên góc ACB = 2.góc ACD = 2.15 = 30 độ
Trong tam giác ABC có góc A + góc B + góc ACB = 180 độ
=> góc B = 180 độ - (góc A + góc ACB) = 180 độ - (90 độ + 30 độ) = 60 độ

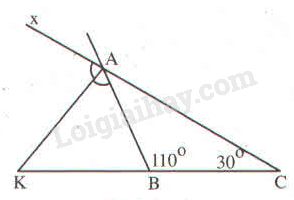
Ta có \(\widehat{xAB}\) là góc ngoài tại đỉnh A của \(\Delta ABC.\)
\(\Rightarrow\widehat{xAB}=\widehat{ABC}+\widehat{ACB}\) (tính chất góc ngoài tam giác).
\(\Rightarrow\widehat{xAB}=110^0+30^0\)
\(\Rightarrow\widehat{xAB}=140^0.\)
Vì \(AK\) là tia phân giác của \(\widehat{BAx}\left(gt\right)\)
\(\Rightarrow\widehat{xAK}=\widehat{KAB}=\frac{\widehat{BAx}}{2}=\frac{140^0}{2}=70^0\) (1)
Lại có: \(\widehat{ABC}+\widehat{ABK}=180^0\) (vì 2 góc kề bù)
\(\Rightarrow110^0+\widehat{ABK}=180^0\)
\(\Rightarrow\widehat{ABK}=180^0-110^0\)
\(\Rightarrow\widehat{ABK}=70^0\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{KAB}=\widehat{ABK}=70^0.\)
Mà 2 góc này thuộc \(\Delta KAB\)
\(\Rightarrow\Delta KAB\) có 2 góc bằng nhau (đpcm).
Chúc bạn học tốt!
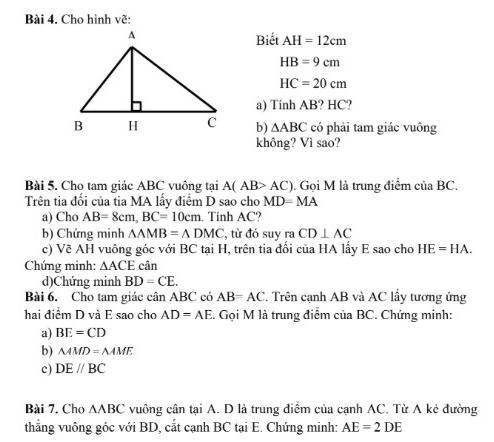
.jpg) Tính số đo góc P1. Nhớ làm rõ ra nha
Tính số đo góc P1. Nhớ làm rõ ra nha