Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ ĐKXĐ: \(x>\frac{1}{2}\)
\(\Leftrightarrow\frac{3x^2-1}{\sqrt{2x-1}}-\sqrt{2x-1}=mx\)
\(\Leftrightarrow\frac{3x^2-2x}{\sqrt{2x-1}}=mx\Leftrightarrow\frac{3x-2}{\sqrt{2x-1}}=m\)
Đặt \(\sqrt{2x-1}=a>0\Rightarrow x=\frac{a^2+1}{2}\Rightarrow\frac{3a^2-1}{2a}=m\)
Xét hàm \(f\left(a\right)=\frac{3a^2-1}{2a}\) với \(a>0\)
\(f'\left(a\right)=\frac{12a^2-2\left(3a^2-1\right)}{4a^2}=\frac{6a^2+2}{4a^2}>0\)
\(\Rightarrow f\left(a\right)\) đồng biến
Mặt khác \(\lim\limits_{a\rightarrow0^+}\frac{3a^2-1}{2a}=-\infty\); \(\lim\limits_{a\rightarrow+\infty}\frac{3a^2-1}{2a}=+\infty\)
\(\Rightarrow\) Phương trình đã cho luôn có nghiệm với mọi m
b/ ĐKXĐ: \(x\ge2\)
\(\Leftrightarrow\sqrt[4]{\left(x-1\right)^2}+4m\sqrt[4]{\left(x-1\right)\left(x-2\right)}+\left(m+3\right)\sqrt[4]{\left(x-2\right)^2}=0\)
Nhận thấy \(x=2\) không phải là nghiệm, chia 2 vế cho \(\sqrt[4]{\left(x-2\right)^2}\) ta được:
\(\sqrt[4]{\left(\frac{x-1}{x-2}\right)^2}+4m\sqrt[4]{\frac{x-1}{x-2}}+m+3=0\)
Đặt \(\sqrt[4]{\frac{x-1}{x-2}}=a\) pt trở thành: \(a^2+4m.a+m+3=0\) (1)
Xét \(f\left(x\right)=\frac{x-1}{x-2}\) khi \(x>0\)
\(f'\left(x\right)=\frac{-1}{\left(x-2\right)^2}< 0\Rightarrow f\left(x\right)\) nghịch biến
\(\lim\limits_{x\rightarrow2^+}\frac{x-1}{x-2}=+\infty\) ; \(\lim\limits_{x\rightarrow+\infty}\frac{x-1}{x-2}=1\) \(\Rightarrow f\left(x\right)>1\Rightarrow a>1\)
\(\left(1\right)\Leftrightarrow m\left(4a+1\right)=-a^2-3\Leftrightarrow m=\frac{-a^2-3}{4a+1}\)
Xét \(f\left(a\right)=\frac{-a^2-3}{4a+1}\) với \(a>1\)
\(f'\left(a\right)=\frac{-2a\left(4a+1\right)-4\left(-a^2-3\right)}{\left(4a+1\right)^2}=\frac{-4a^2-2a+12}{\left(4a+1\right)^2}=0\Rightarrow a=\frac{3}{2}\)
\(f\left(1\right)=-\frac{4}{5};f\left(\frac{3}{2}\right)=-\frac{3}{4};\) \(\lim\limits_{a\rightarrow+\infty}\frac{-a^2-3}{4a+1}=-\infty\)
\(\Rightarrow f\left(a\right)\le-\frac{3}{4}\Rightarrow m\le-\frac{3}{4}\)

a)\(\log_{\frac{2}{x}}x^2-14\log_{16x}x^3+40\log_{4x}\sqrt{x}=0\)ĐKXĐ: x>0
\(\Leftrightarrow2\log_{\frac{2}{x}}x-42\log_{16x}+20\log_{4x}\sqrt{x}=0\)
\(\Leftrightarrow\frac{2}{\log_x\frac{2}{x}}-\frac{42}{\log_x16x}+\frac{20}{\log_x4x}=0\)
\(\Leftrightarrow\frac{2}{\log_x2-1}-\frac{42}{4\log_x2+1}+\frac{20}{2\log_x+1}=0\)
Đặt \(\log_x2=a\left(a\in R\right)\)
Thay vào pt:\(\frac{2}{a-1}-\frac{42}{4a+1}+\frac{20}{2a+1}=0\)
\(\Leftrightarrow2a^2-a+4=0\)(pt này vô nghiệm)
Vậy pt đã cho vô nghiệm

d) Điều kiện \(\begin{cases}x\ne0\\\log_2\left|x\right|\ge0\end{cases}\)\(\Leftrightarrow\left|x\right|\ge\)1
Phương trình đã cho tương đương với :
\(\log_2\left|x\right|^{\frac{1}{2}}-4\sqrt{\log_{2^2}\left|x\right|}-5=0\)
\(\Leftrightarrow\frac{1}{2}\log_2\left|x\right|-4\sqrt{\frac{1}{4}\log_2\left|x\right|}-5=0\)
Đặt \(t=\sqrt{\frac{1}{2}\log_2\left|x\right|}\) \(\left(t\ge0\right)\) thì phương trình trở thành :
\(t^2-4t-5=0\) hay t=-1 V t=5
Do \(t\ge0\) nên t=5
\(\Rightarrow\frac{1}{2}\log_2\left|x\right|=25\Leftrightarrow\log_2\left|x\right|=50\Leftrightarrow\left|x\right|=2^{50}\) Thỏa mãn
Vậy \(x=\pm2^{50}\) là nghiệm của phương trình
c) Điều kiện x>0. Phương trình đã cho tương đương với :
\(x^{lg^2x^2-3lgx-\frac{9}{2}}=\left(10^{lgx}\right)^{-2}\)
\(\Leftrightarrow lg^2x^2-3lgx-\frac{9}{2}=-2\)
\(\Leftrightarrow8lg^2x-6lgx-5=0\)
Đặt \(t=lgx\left(t\in R\right)\) thì phương trình trở thành
\(8t^2-6t-5=0\) hay\(t=-\frac{1}{2}\) V \(t=\frac{5}{4}\)
Với \(t=-\frac{1}{2}\) thì \(lgx=-\frac{1}{2}\Leftrightarrow x=\frac{1}{\sqrt{10}}\)
Với \(t=\frac{5}{4}\) thì \(lgx=\frac{5}{4}\Leftrightarrow x=\sqrt[4]{10^5}\)
Vậy phương trình đã cho có nghiệm \(x=\sqrt[4]{10^5}\) và \(x=\frac{1}{\sqrt{10}}\)

d) Đưa 2 vế về cùng cơ số 2, ta được
\(2^{-3}.2^{4x-6}=\left(2^{\frac{-5}{2}}\right)^x\) hay \(2^{4x-9}=2^{\frac{5}{2}x}\)
Do đó :
\(4x-9=\frac{5}{2}x\Leftrightarrow\frac{3}{2}x=9\Leftrightarrow x=6\)
Vậy phương trình đã cho chỉ có 1 nghiệm x=6
c) Phương trình đã cho tương đương với :
\(\frac{1}{4}.4^x+16.4^x=10\Leftrightarrow\frac{33}{2}.4^x=10\Leftrightarrow4^x=\frac{20}{33}\Leftrightarrow x=\log_4\frac{20}{33}\)
Vậy nghiệm của phương trình là \(x=\log_4\frac{20}{33}\)

a) Đặt t = 13x > 0 ta được phương trình:
13t2 – t – 12 = 0 ⇔ (t – 1)(13t + 12) = 0
⇔ t = 1 ⇔ 13x = 1 ⇔ x = 0
b)
Chia cả hai vế phương trình cho 9x ta được phương trình tương đương
(1+(23)x)(1+3.(23)x)=8.(23)x(1+(23)x)(1+3.(23)x)=8.(23)x
Đặt t=(23)xt=(23)x (t > 0) , ta được phương trình:
(1 + t)(1 + 3t) = 8t ⇔ 3t2 – 4t + 1 = 0 ⇔ t∈{13,1}t∈{13,1}
Với t=13t=13 ta được nghiệm x=log2313x=log2313
Với t = 1 ta được nghiệm x = 0
c) Điều kiện: x > 2
Vì nên phương trình đã cho tương đương với:
[log3(x−2)=0log5x=1⇔[x=3x=5[log3(x−2)=0log5x=1⇔[x=3x=5
d) Điều kiện: x > 0
log22x – 5log2x + 6 = 0
⇔(log2x – 2)(log2x – 3) = 0
⇔ x ∈ {4, 8}
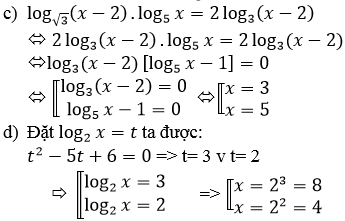
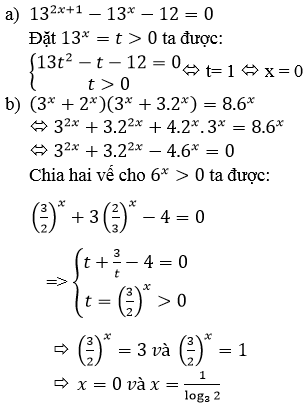
a)
Đặt \(\frac{x}{2}=t\Rightarrow 3^{2t}-4=5^t\)
\(\Leftrightarrow 9^t-5^t=4\)
TH1: \(t>1\Rightarrow 9^t-5^t< 4^t\)
\(\Leftrightarrow 9^t< 4^t+5^t\)
\(\Leftrightarrow 1< \left(\frac{4}{9}\right)^t+\left(\frac{5}{9}\right)^t\) \((*)\)
Ta thấy vì \(\frac{4}{9};\frac{5}{9}<1 \), do đó với \(t>1\Rightarrow \left\{\begin{matrix} \left(\frac{4}{9}\right)^t< \frac{4}{9}\\ \left(\frac{5}{9}\right)^t< \frac{5}{9}\end{matrix}\right.\)
\(\Rightarrow \left(\frac{4}{9}\right)^t+\left(\frac{5}{9}\right)^t< \frac{4}{9}+\frac{5}{9}=1\) (mâu thuẫn với (*))
TH2: \(t<1 \) tương tự TH1 ta cũng suy ra mâu thuẫn
do đó \(t=1\Rightarrow x=2\)
b)
Ta có: \(5^{2x}=3^{2x}+2.5^x+2.3^x\)
\(\Leftrightarrow (5^{2x}-2.5^{x}+1)=3^{2x}+2.3^x+1\)
\(\Leftrightarrow (5^x-1)^2=(3^x+1)^2\)
\(\Leftrightarrow (5^x-3^x-2)(5^x+3^x)=0\)
Dễ thấy \(5^x+3^x>0\forall x\in\mathbb{R}\Rightarrow 5^x-3^x-2=0\)
\(\Leftrightarrow 5^x-3^x=2\)
\(\Leftrightarrow 5^x=3^x+2\)
Đến đây ta đưa về dạng giống hệt phần a, ta thu được nghiệm \(x=1\)
c)
\((2-\sqrt{3})^x+(2+\sqrt{3})^x=4^x\)
\(\Leftrightarrow \left(\frac{2-\sqrt{3}}{4}\right)^x+\left(\frac{2+\sqrt{3}}{4}\right)^x=1\)
TH1: \(x>1\)
Vì \(\frac{2+\sqrt{3}}{4};\frac{2-\sqrt{3}}{4}<1;x> 1 \Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x< \frac{2-\sqrt{3}}{4};\left ( \frac{2+\sqrt{3}}{4} \right )^x< \frac{2+\sqrt{3}}{4}\)
\(\Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x+\left ( \frac{2+\sqrt{3}}{4} \right )^x<\frac{2-\sqrt{3}}{4}+\frac{2+\sqrt{3}}{4}=1\) (vô lý)
TH2: \(x<1 \)
\(\frac{2+\sqrt{3}}{4};\frac{2-\sqrt{3}}{4}<1; x< 1 \Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x> \frac{2-\sqrt{3}}{4};\left ( \frac{2+\sqrt{3}}{4} \right )^x> \frac{2+\sqrt{3}}{4}\)
\(\Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x+\left ( \frac{2+\sqrt{3}}{4} \right )^x>\frac{2-\sqrt{3}}{4}+\frac{2+\sqrt{3}}{4}=1\) (vô lý)
Do đó \(x=1\)