Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải hệ sau :
Câu a :
\(\left\{{}\begin{matrix}x+y=-1\\2x+y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=-1\\-x=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=-1\\x=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)
Vậy ...........................
Câu b :
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x}=a\\\dfrac{1}{y}=b\end{matrix}\right.\) . Ta có :
\(\left\{{}\begin{matrix}a+b=\dfrac{1}{5}\\3a+4b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+3b=\dfrac{3}{5}\\3a+4b=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-b=-\dfrac{7}{5}\\3a+4b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{7}{5}\\a=-\dfrac{6}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{7}{5}\\\dfrac{1}{y}=-\dfrac{6}{5}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{7}\\y=-\dfrac{5}{6}\end{matrix}\right.\)
Vậy..................
\(a,\left\{{}\begin{matrix}2x-y=4\\x+5y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y=4\\2x+10y=6\end{matrix}\right.\left\{{}\begin{matrix}11y=2\\2x+10y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2}{11}\\2x+10.\dfrac{2}{11}=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2}{11}\\2x=\dfrac{46}{11}\end{matrix}\right.\left\{{}\begin{matrix}y=\dfrac{2}{11}\\x=\dfrac{23}{11}\end{matrix}\right.\)

a: \(\Leftrightarrow\left\{{}\begin{matrix}\left(x+2\right)\left(y+3\right)-xy=100\\xy-\left(x-2\right)\left(y-2\right)=64\end{matrix}\right.\)
=>xy+3x+2y+6-xy=100 và xy-xy+2x+2y-4=64
=>3x+2y=94 và 2x+2y=68
=>x=26 và x+y=34
=>x=26 và y=8
b: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3x+3+2}{x+1}-\dfrac{2}{y+4}=4\\\dfrac{2x+2-2}{x+1}-\dfrac{5y+20-11}{y+4}=9\end{matrix}\right.\)
=>\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x+1}-\dfrac{2}{y+4}=4-3=1\\\dfrac{-2}{x+1}+\dfrac{11}{y+4}=9+5-2=12\end{matrix}\right.\)
=>x+1=18/35; y+4=9/13
=>x=-17/35; y=-43/18

a) \(\left\{{}\begin{matrix}\dfrac{x+1}{x-1}+\dfrac{3y}{y+2}=7\left(1\right)\\\dfrac{2}{x-1}-\dfrac{5}{y+2}=4\left(2\right)\end{matrix}\right.\)ĐK: \(x\ne1;y\ne-2\)
(1)\(\Leftrightarrow1+\dfrac{2}{x-1}+3-\dfrac{6}{y+2}=7\Leftrightarrow\dfrac{2}{x-1}-\dfrac{6}{y+2}=3\)
Đặt \(A=\dfrac{1}{x-1};B=\dfrac{1}{y+2}\)
\(\Rightarrow\left\{{}\begin{matrix}2A-6B=3\\2A-5B=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{11}{9}\\y=-1\end{matrix}\right.\)(TM)
Vậy hpt có nghiệm là \(\left(\dfrac{11}{9};-1\right)\).
b)ĐK: \(y\ge-1\)
Đặt \(A=x^2-2x;B=\sqrt{y+1}\left(B\ge0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}2A+B=0\\3A-2B=-7\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}A=-1\\B=2\end{matrix}\right.\)(TM)
\(\Rightarrow\left\{{}\begin{matrix}x=\pm1\\y=1\end{matrix}\right.\)
Vậy hpt có nghiệm là (-1;1);(1;1).

Bài 1 : Ta xét : \(\dfrac{2}{4}=\dfrac{3}{6}=\dfrac{5}{10}\) hay \(\dfrac{a}{a'}=\dfrac{b}{b'}=\dfrac{c}{c'}\)
Nên phương trình có vô số nghiệm .
Mà \(2x+3y=5\Rightarrow x=\dfrac{5-3y}{2}\)
Vậy \(y\in R\) và \(x=\dfrac{5-3y}{2}\)
Bài 2 : \(\left\{{}\begin{matrix}\dfrac{3x}{x+1}-\dfrac{2}{y+4}=4\\\dfrac{2x}{x+1}-\dfrac{5}{y+4}=9\end{matrix}\right.\)
Đặt \(\dfrac{x}{x+1}=a\) và \(\dfrac{1}{y+4}=b\) Khi đó hệ trở thành :
\(\left\{{}\begin{matrix}3a-2b=4\\2a-5b=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6a-4b=8\\6a-15b=27\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}11b=-19\\6a-4b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-\dfrac{19}{11}\\a=\dfrac{2}{11}\end{matrix}\right.\)
Với \(\left\{{}\begin{matrix}a=\dfrac{2}{11}\\b=-\dfrac{19}{11}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{x+1}=\dfrac{2}{11}\\\dfrac{1}{y+4}=-\dfrac{19}{11}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}11x=2x+2\\-19y-76=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=2\\-19y=87\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{9}\\y=-\dfrac{87}{19}\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(\dfrac{2}{9};-\dfrac{87}{19}\right)\)

c: =>3x^2+3y^2=39 và 3x^2-2y^2=-6
=>5y^2=45 và x^2=13-y^2
=>y^2=9 và x^2=4
=>\(\left\{{}\begin{matrix}x\in\left\{2;-2\right\}\\y\in\left\{3;-3\right\}\end{matrix}\right.\)
d: \(\Leftrightarrow\left\{{}\begin{matrix}5\sqrt{x}=5\\\sqrt{x}-\sqrt{y}=-\dfrac{11}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\\sqrt{y}=1+\dfrac{11}{2}=\dfrac{13}{2}\end{matrix}\right.\)
=>x=1 và y=169/4
b: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3x+3-3}{x+1}-\dfrac{2}{y+4}=4\\\dfrac{2x+2-2}{x+1}-\dfrac{5}{y+4}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{3}{x+1}-\dfrac{2}{y+4}=4-3=1\\-\dfrac{2}{x+1}-\dfrac{5}{y+4}=9-2=7\end{matrix}\right.\)
=>x+1=11/9 và y+4=-11/19
=>x=2/9 và y=-87/19


 Còn lại tương tự
Còn lại tương tự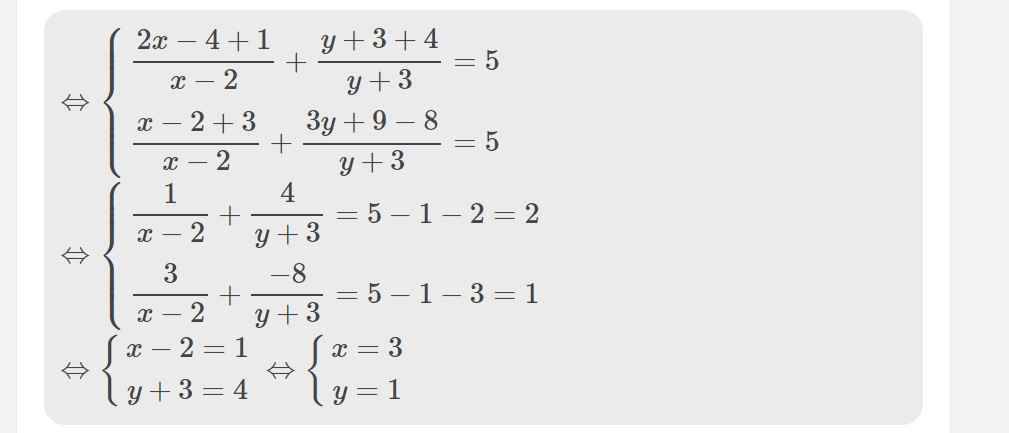
a, \(\left\{{}\begin{matrix}2x+2y=4\\2x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5y=-5\\x=2-y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=3\end{matrix}\right.\)
b, \(\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{3}\\x+y=10\end{matrix}\right.\)Theo tc dãy tỉ số bằng nhau
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{x+y}{2+3}=\dfrac{10}{5}=2\Rightarrow x=4;y=6\)
a.\(\Leftrightarrow\left\{{}\begin{matrix}3x+3y=6\\2x-3y=9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}5x=15\\2x-3y=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\2.3-3y=9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)
b.\(\Leftrightarrow\left\{{}\begin{matrix}3x=2y\\x+y-10=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x-2y=0\\x+y-10=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x-2y=0\\2x+2y=20\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}5x=20\\3x-2y=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=4\\3.4-2y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=6\end{matrix}\right.\)