Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \({x^2} + x - 6 \le 0\) là một bất phương trình bậc hai một ẩn
Vì \({2^2} + 2 - 6 = 0\) nên \(x = 2\) là nghiệm của bất phương trình trên
b) \(x + 2 > 0\) không là bất phương trình bậc hai một ẩn
c) \( - 6{x^2} - 7x + 5 > 0\) là một bất phương trình bậc hai một ẩn
Vì \( - {6.2^2} - 7.2 + 5 = - 33 < 0\) nên \(x = 2\) không là nghiệm của bất phương trình trên

\(2x-1\le0\Rightarrow x\le\frac{1}{2}\)
\(\left(1-x\right)\left(x-2\right)>0\Rightarrow1< x< 2\)
\(\left(2-x\right)\left(x^2-2x+3\right)< 0\)
\(\Leftrightarrow2-x< 0\) (do \(x^2-2x+3=\left(x-1\right)^2+2>0\) \(\forall x\))
\(\Leftrightarrow x>2\)

a) Tam thức \(f(x) = {x^2} - 1\) có \(\Delta = 4 > 0\)nên f(x) có 2 nghiệm phân biệt \({x_1} = - 1;{x_2} = 1\)
Mặt khác a=1>0, do đó ta có bảng xét dấu:

Tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ {1; + \infty } \right)\)
b) Tam thức \(g(x) = {x^2} - 2x - 1\) có \(\Delta = 8 > 0\) nên g(x) có 2 nghiệm phân biệt \({x_1} = 1 - \sqrt 2 ;{x_2} = 1 + \sqrt 2 \)
Mặt khác a = 1 > 0, do đó ta có bảng xét dấu:

Tập nghiệm của bất phương trình là \(\left( {1 - \sqrt 2 ;1 + \sqrt 2 } \right)\)
c) Tam thức \(h(x) = - 3{x^2} + 12x + 1\) có\(\Delta ' = 39 > 0\)nên h(x) có 2 nghiệm phân biệt \({x_1} = \frac{{6 - \sqrt {39} }}{3};{x_2} = \frac{{6 + \sqrt {39} }}{3}\)
Mặt khác a = -3 < 0, do đó ta có bảng xét dấu:

Tập nghiệm của bất phương trình là \(\left( { - \infty ; \frac{{6 - \sqrt {39} }}{3}} \right] \cup \left[ {\frac{{6 + \sqrt {39} }}{3}; + \infty } \right)\)
d) Tam thức \(k(x) = 5{x^2} + x + 1\) có \(\Delta = - 19 < 0\), hệ số a=5>0 nên k(x) luôn dương ( cùng dấu với a) với mọi x, tức là \(5{x^2} + x + 1 > 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm


1. \(\Leftrightarrow\left(2x-1\right)\left(3x+1\right)< 0\)
\(\Rightarrow-\frac{1}{3}< x< \frac{1}{2}\)
2. \(\Leftrightarrow\left(x-2\right)\left(3-2x\right)>0\)
\(\Rightarrow\frac{3}{2}< x< 2\)
3. \(\Leftrightarrow\left(5x-3\right)^2>0\)
\(\Rightarrow x\ne\frac{3}{5}\)
4. \(\Leftrightarrow-3\left(x-\frac{1}{6}\right)-\frac{59}{12}< 0\)
\(\Rightarrow x\in R\)
5. \(\Leftrightarrow2\left(x-1\right)^2+5\ge0\)
\(\Rightarrow x\in R\)
6. \(\Leftrightarrow\left(x+2\right)\left(8x+7\right)\le0\)
\(\Rightarrow-2\le x\le-\frac{7}{8}\)
7.
\(\Leftrightarrow\left(x-1\right)^2+2>0\)
\(\Rightarrow x\in R\)
8. \(\Leftrightarrow\left(3x-2\right)\left(2x+1\right)\ge0\)
\(\Rightarrow\left[{}\begin{matrix}x\le-\frac{1}{2}\\x\ge\frac{2}{3}\end{matrix}\right.\)
9. \(\Leftrightarrow\frac{1}{3}\left(x+3\right)\left(x+6\right)< 0\)
\(\Rightarrow-6< x< -3\)
10. \(\Leftrightarrow x^2-6x+9>0\)
\(\Leftrightarrow\left(x-3\right)^2>0\)
\(\Rightarrow x\ne3\)

a) Xét tam thức \(f\left( x \right) = 7{x^2} - 19x - 6\) có \(\Delta = 529 > 0\), có hai nghiệm phân biệt \({x_1} = - \frac{2}{7},{x_2} = 3\) và có \(a = 7 > 0\)
Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là đoạn \(\left[ { - \frac{2}{7};3} \right]\)
b) \( - 6{x^2} + 11x > 10 \Leftrightarrow - 6{x^2} + 11x - 10 > 0\)
Xét tam thức \(f\left( x \right) = - 6{x^2} + 11x - 10\) có \(\Delta = - 119 < 0\)và có \(a = - 6 < 0\)
Ta có bảng xét dấu như sau

Vậy bất phương trình vô nghiệm
c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1 \Leftrightarrow 2{x^2} - 6x + 6 > 0\)
Xét tam thức \(f\left( x \right) = 2{x^2} - 6x + 6\) có \(\Delta = - 12 < 0\)và có \(a = 2 > 0\)
Ta có bảng xét dấu như sau
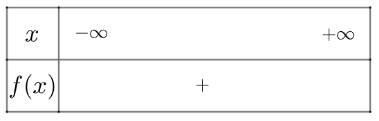
Vậy bất phương trình có vô số nghiệm
d) Xét tam thức \(f\left( x \right) = {x^2} - 10x + 25\) có \(\Delta = 0\), có nghiệm kép \({x_1} = {x_2} = 5\) và có \(a = 1 > 0\)
Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là \(x = 5\)
a) Tam thức \(f(x) = - 5{x^2} + x - 1\) có \(\Delta = - 19 < 0\), hệ số \(a = - 5 < 0\) nên f(x) luôn âm (cùng dấu với a) với mọi x, tức là \(\)\( - 5{x^2} + x - 1 < 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm
b) Tam thức \(g(x) = {x^2} - 8x + 16\) có \(\Delta = 0\), hệ số a=1>0 nên g(x) luôn dương (cùng dấu với a) với mọi \(x \ne 4\), tức là \({x^2} - 8x + 16 > 0\) với mọi \(x \ne 4\)
Suy ra bất phương trình có nghiệm duy nhất là x = 4
c) Tam thức \(h(x) = {x^2} - x + 6\) có \(\Delta = - 23 < 0\), hệ số a=1>0 nên h(x) luôn dương (cùng dấu với a) với mọi x, tức là \({x^2} - x + 6 > 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm.