BB
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HY
2 tháng 4 2017
a, \(\left|5x-4\right|\ge6\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-4\ge6\\5x-4\le-6\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge2\\x\le-\dfrac{2}{5}\end{matrix}\right.\)
Q
2 tháng 4 2017
a) <=> (5x - 2)2 ≥ 62 <=> (5x – 4)2 – 62 ≥ 0
<=> (5x - 4 + 6)(5x - 4 - 6) ≥ 0 <=> (5x + 2)(5x - 10) ≥ 0
Bảng xét dấu:
Từ bảng xét dấu cho tập nghiệm của bất phương trình:
T = ∪ [2; +∞).
b) <=>
<=>
<=>
<=>
Tập nghiệm của bất phương trình T = (-∞; - 5) ∪ (- 1; 1) ∪ (1; +∞).
6 tháng 4 2017
a) \(x^2\ge4x\)(1)
Nếu \(\left[{}\begin{matrix}x_1=0\\x_2=4\end{matrix}\right.\) \(\Rightarrow VT=VP\)
Nếu \(x< 0\Rightarrow VT>0;VP< 0\)=> \(VT>VP\)
Nếu 0<x<4 \(\Rightarrow VT< VP\)
nếu x> 4\(\Rightarrow VT>VP\)
Kết luận nghiệm BPT (1): \(\left[{}\begin{matrix}x\le0\\x\ge4\end{matrix}\right.\)
b)
(1) \(\Rightarrow\left[{}\begin{matrix}x< \dfrac{3-\sqrt{5}}{2}\\x>\dfrac{3+\sqrt{5}}{2}\end{matrix}\right.\)
(2) \(\Rightarrow-2\le x\le3\)
KL nghiệm
\(\left[{}\begin{matrix}-2\le x< \dfrac{3-\sqrt{5}}{2}\\\dfrac{3+\sqrt{5}}{2}< x\le3\end{matrix}\right.\)
BT
9 tháng 5 2017
a)\(Bpt\Leftrightarrow\) \(\left\{{}\begin{matrix}x^2-4x\ge0\left(1\right)\\\left(2x-1\right)^2-9>0\left(2\right)\end{matrix}\right.\)
Giải (1): \(x^2-4x\ge0\Leftrightarrow\left[{}\begin{matrix}x\ge4\\x\le0\end{matrix}\right.\)
Giải (2): \(\left(2x-1\right)^2-9=\left(2x-1\right)^2-3^2=\left(2x-4\right)\left(2x+2\right)\)
\(\left(2x-4\right)\left(2x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Vì vậy: \(\left(2x-1\right)^2-9< 0\Leftrightarrow-1< x< 2\).
Kết hợp điều kiện \(\left(1\right)\) và \(\left(2\right)\) suy ra: \(-1< x\le0\) thỏa mãn hệ bất phương trình.
CC
0
15 tháng 4 2017
a) - x + 2 + 2(y - 2) < 2(1 - x) <=> y <
Tập nghiệm của bất phương trình là:
T = {(x, y)|x ∈ R; y < }.
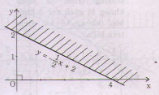
Để biểu diễn tập nghiệm T trên mặt phẳng tọa độ, ta thực hiện:
+ Vẽ đường thẳng (d): y=
+ Lấy điểm gốc tọa độ O(0; 0) (d).
Ta thấy: 0 < - 0 + 2. Chứng tỏ (0; 0) là một nghiệm của bất phương trình. Vậy nửa mặt phẳng bờ là đường thẳng (d) (không kể bờ) chứa gốc O(0; 0) là tập hợp các điểm biểu diễn tập nghiệm của bất phương trình đã cho (nửa mặt phẳng không bị gạch sọc)
S
3 tháng 8 2019
\(6\sqrt{x^2-34x+64}=x^2-34x+48\)
\(\text{đ}at:x^2-34x+48=a\Rightarrow6\sqrt{a+16}=a\Leftrightarrow36a+576=a^2\Leftrightarrow a^2-36a-576=0;\Delta=\left(-36\right)^2-4.\left(-576\right).1=3600\Rightarrow\left\{{}\begin{matrix}a_1=24\\a_2=-96\end{matrix}\right.\)
\(+,a=-96\Rightarrow x^2-34x+48=-96\Leftrightarrow x^2-34x+144=0;\Delta=34^2-4.144=580\Rightarrow\left\{{}\begin{matrix}x_1=-34+2\sqrt{145}\\x_2=-34-2\sqrt{145}\end{matrix}\right.\)
\(+,a=24\Rightarrow x^2-34x+48=24\Leftrightarrow x^2-34x+24=0;\Delta=1156-96=1060\Rightarrow\left\{{}\begin{matrix}x_1=-34+2\sqrt{265}\\x_2=-34-2\sqrt{265}\end{matrix}\right.\)
BT
2
|x - 6| < x2 - 5x + 9 (1)
Xét 2 trường hợp:
* Với x - 6 \(\ge0\) => x \(\ge6\) , (1) trở thành: x - 6 < x2 - 5x + 9 => x2 - 6x + 15 > 0
Có: pt x2 - 6x + 15 có \(\Delta<0\) => x2 - 6x + 15 > 0 với mọi x thuộc R
=> S1 = [6 ; +\(\infty\))
* Với x - 6 < 0 => x < 6 , (1) trở thành: 6 - x < x2 - 5x + 9 => x2 - 4x + 3 > 0
Lập bảng xét dấu:
=> x2 - 4x + 3 > 0 khi x \(\in\) (-\(\infty\); 1) \(\cup\) (3 ; +\(\infty\))
=> S2 = (- \(\infty\); 1) \(\cup\) (3 ; 6)
Vậy S = S1 \(\cup\) S2 = (- \(\infty\) ; 1) \(\cup\)(3 ; 6]