Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tứ giác ANHM có 3 góc vuông : AMH ; MAN ; ANH nên là hình chữ nhật
b) Hình chữ nhật ANHM có AH cắt MN tại trung điểm mỗi đường nên OA =\(\frac{AH}{2};ON=\frac{MN}{2}\)mà AH = MN nên OA = ON
\(\Rightarrow\Delta OAN\)cân tại O (1)
Ta lại có :\(\Delta ABC,\Delta AHC\)lần lượt vuông tại A,H có\(\widehat{B}+\widehat{C}=\widehat{HAC}+\widehat{C}=90^0\Rightarrow\widehat{B}=\widehat{OAN}=\widehat{ONA}\)(do 1)
mà\(\widehat{ONA}+\widehat{ONC}=180^0\)(kề bù).Vậy tứ giác BCNM có\(\widehat{B}+\widehat{MNC}=180^0\Rightarrow\widehat{C}+\widehat{BMN}=180^0\)
c)\(\Delta ANM,\Delta ABC\)cùng vuông tại A có\(\widehat{B}=\widehat{MNA}\Rightarrow\Delta ANM~\Delta ABC\left(g-g\right)\Rightarrow\frac{AN}{AM}=\frac{AB}{AC}\)=> AM.AB = AN.AC
d)\(\Delta ABC\)vuông tại A có I là trung điểm BC nên trung tuyến AI =\(\frac{BC}{2}\)mà BI =\(\frac{BC}{2}\)nên AI = BI
\(\Rightarrow\Delta ABI\)cân tại I =>\(\widehat{BAI}=\widehat{B}=\widehat{MNA}\)mà\(\Delta AMN\)vuông tại A có\(\widehat{AMN}+\widehat{MNA}=90^0\)
Gọi giao điểm AI và MN là P thì\(\Delta AMP\)có \(\widehat{MAP}+\widehat{AMP}=90^0\)nên\(\Delta AMP\)vuông tại P => AI _|_ MN

Bài 2:
Ta có: AM=1/2BC
nên AM=BM=CM
Xét ΔMAB có MA=MB
nên ΔMAB cân tại M
=>\(\widehat{MAB}=\widehat{B}\)
Xét ΔMAC có MA=MC
nên ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{C}\)
Xét ΔBAC có \(\widehat{BAC}+\widehat{B}+\widehat{C}=180^0\)
\(\Leftrightarrow\widehat{MAB}+\widehat{B}+\widehat{MAC}+\widehat{C}=180^0\)
\(\Leftrightarrow2\cdot\left(\widehat{MAB}+\widehat{MAC}\right)=180^0\)
=>\(\widehat{BAC}=90^0\)
hay ΔABC vuông tại A

a, Xét tg AHI và tg AKI ta có:
góc H = góc K = 90
AI là cạnh chung
góc HAI = góc KAI ( AI là tia phân giác góc BAC)
=> tg AHI =tg AKI ( cạnh huyền-góc nhọn)
=> AH=AK

Hình vẽ:

Lời giải:
a)
HM⊥AB;HN⊥AC⇒HMAˆ=HNAˆ=900HM⊥AB;HN⊥AC⇒HMA^=HNA^=900
Xét tứ giác AMHNAMHN có tổng 2 góc đối HMAˆ+HNAˆ=900+900=1800HMA^+HNA^=900+900=1800 nên AMHNAMHN là tứ giác nội tiếp (đpcm)
b)
Vì AMHNAMHN nội tiếp ⇒AMNˆ=AHNˆ⇒AMN^=AHN^
Mà AHNˆ=ACBˆ(=900−NHCˆ)AHN^=ACB^(=900−NHC^)
⇒AMNˆ=ACBˆ⇒AMN^=ACB^
Xét tam giác AMNAMN và ACBACB có:
{Aˆ−chungAMNˆ=ACBˆ(cmt)⇒△AMN∼△ACB(g.g){A^−chungAMN^=ACB^(cmt)⇒△AMN∼△ACB(g.g)
⇒AMAC=ANAB⇒AM.AB=AC.AN⇒AMAC=ANAB⇒AM.AB=AC.AN (đpcm)
c)
Ta có: ACBˆ=AEBˆACB^=AEB^ (góc nội tiếp chắn cung ABAB)
ACBˆ=AMNˆACB^=AMN^ (cmt)
⇒AEBˆ=AMNˆ⇒AEB^=AMN^
⇔IEBˆ=1800−BMIˆ⇔IEB^=1800−BMI^
⇔IEBˆ+BMIˆ=1800⇔IEB^+BMI^=1800, do đó tứ giác BMIEBMIE nội tiếp
⇒MIEˆ=1800−MBEˆ=1800−900=900⇒MIE^=1800−MBE^=1800−900=900 (MBEˆ=ABEˆ=900MBE^=ABE^=900 vì là góc nt chắn nửa đường tròn)
⇒MN⊥AE⇒MN⊥AE . Ta có đpcm.
~Hok tốt~
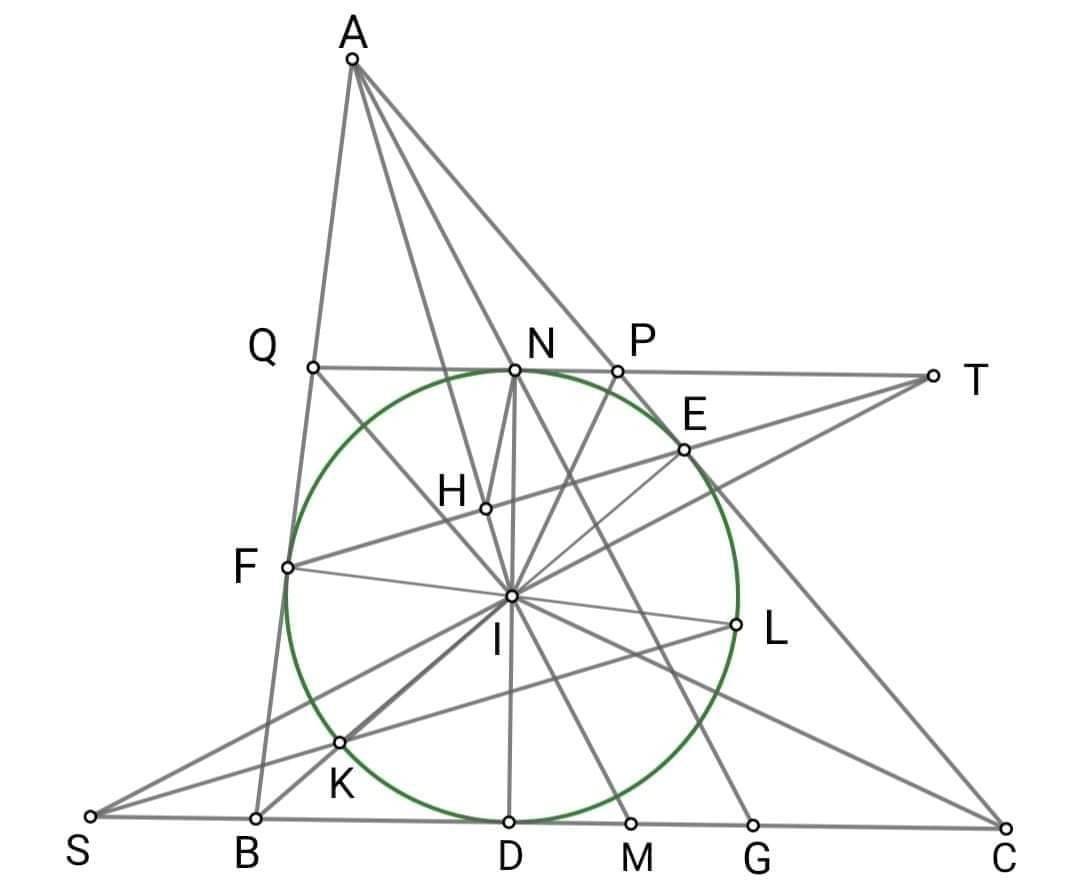
HÌnh bạn tự vẽ.
Bổ đề: (định lý Ptô-lê-mê)
Trong một tứ giác nội tiếp ABCD, ta có:
AC . BD = AB . CD + BC . AD
Áp dụng bổ đề trên cho tứ giác nội tiếp IPAN, ta có IA.NP = IP.AN + IN.AP = 2r(p - a) (ở đây ta đặt BC = a, CA = b, AB = c) và
\(p=\frac{a+b+c}{2}\) thì AN = AP = p - a.
Tương tự IB . PM = 2r(p - b)
IC . MN = 2r(p - c)
Nhân theo vế ba đẳng thức trên ta được:
\(IA.IB.IC.MN.NP.PM=8r^3\left(p-a\right)\left(p-b\right)\left(p-c\right)\).
Mặt khác, vì r là bán kính đường tròn ngoại tiếp \(\Delta MNP\)nên MN.NP.PM = \(4rS_{MNP}\).
Ngoài ra theo công thức Hê-rông ta có:
\(S_{ABC}=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\).Do đó:
IA . IB . IC. 4rSMNP = \(\frac{8r^3.S^2_{ABC}}{p}=8r^4S_{ABC}\)(vì SABC = pr), suy ra đpcm
P/s: Chỗ nào không hiểu thì bạn chỉ việc vẽ hình ra và quan sát hình là được :))