Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình đường thẳng BC: a(x-2) + b(y-2)=0
cos(BA;BC)=cos\(45^0\)=\(\dfrac{1}{\sqrt{2}}=\dfrac{\left|a-b\right|}{\sqrt{2\left(a^2+b^2\right)}}\)
\(\Leftrightarrow\left[{}\begin{matrix}a=0\\b=0\end{matrix}\right.\). Vì a,b không đồng thời bằng 0 nên suy ra \(\left[{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)
Vì tọa độ C có hoành độ x lớn hơn 2 nên phương trình đường thẳng BC là y=2.
Ta có:\(S_{ABC}=\dfrac{1}{2}AB.BC.sin45^0\)\(\Leftrightarrow2=\dfrac{1}{2}\sqrt{8}\sqrt{\left(x_C-2\right)^2}.\dfrac{\sqrt{2}}{2}\Leftrightarrow x_C=4\)
Vậy tọa độ C(4;2)

Chọn B.
*) AH là đường cao của tam giác ABC.
*) Lập phương trình cạnh BC
B(1;-1), C(5;2) 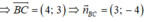
(BC): 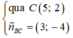
⇒ 3.(x - 5) - 4.(y - 2) = 0 ⇔ 3x - 15 - 4y + 8 = 0 ⇔ 3x - 4y - 7 = 0
Ta có:
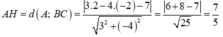

a) \(\overrightarrow{AB}\left(2;2\right);\overrightarrow{AC}\left(2;-2\right)\) . Vì \(\frac{2}{2}\ne\frac{2}{-2}\) nên \(\overrightarrow{AB};\overrightarrow{AC}\) không cùng phương => A; B; C không thẳng hàng
b) Gọi G là trọng tâm tam giác ABC => \(\begin{cases}x_G=\frac{x_A+x_B+x_C}{3}=\frac{-1+1+1}{3}=\frac{1}{3}\\y_G=\frac{y_A+y_B+y_C}{3}=\frac{1+3+\left(-1\right)}{3}=1\end{cases}\)=> G(1/3; 1)
c) ABCD là hình bình hành <=> \(\overrightarrow{AD}=\overrightarrow{BC}\Leftrightarrow\begin{cases}x_D-x_A=x_C-x_B\\y_D-y_A=y_C-y_B\end{cases}\) <=> \(\begin{cases}x_D+1=0\\y_D-1=-4\end{cases}\) <=> \(\begin{cases}x_D=-1\\y_D=-3\end{cases}\) Vậy D (-1;-3)
d) \(\overrightarrow{AB}\left(2;2\right);\overrightarrow{AC}\left(2;-2\right)\)
=> \(\overrightarrow{AB}.\overrightarrow{AC}=2.2+2.\left(-2\right)=0\) => \(\overrightarrow{AB};\overrightarrow{AC}\) vuông góc với nhau => tam giác ABC vuông tại A
Ta có: AB2 = 22 + 22 = 8 ; AC2 = 22 + (-2)2 = 8 => AB = AC => Tam giác ABC cân tại A
vậy...
e) Có thể đề của bạn là tam giác ABE vuông cân tại E ( Khi đó giải điều kiện: EA = EB và vec tơ EA . Vec tơ EB = 0)
g) M nằm trên Ox => M (m; 0)
Tam giác OMA cân tại O <=> OM = OA Hay OM2 = OA2 <=> m2 = (-1)2 + 12 => m2 = 2 <=> m = \(\sqrt{2}\) hoặc m = - \(\sqrt{2}\)
Vậy M (\(\sqrt{2}\); 0) ; M (-\(\sqrt{2}\); 0 )

Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x+y+1=0\\x-2y-2=0\end{matrix}\right.\) \(\Rightarrow B\left(0;-1\right)\)
Gọi vtpt của đường thẳng CM (cũng là đường cao kẻ từ C) có tọa độ \(\left(a;b\right)\)
H là chân đường cao kẻ từ B
\(cos\widehat{HBC}=\dfrac{\left|1.1+1.\left(-2\right)\right|}{\sqrt{1^2+1^2}.\sqrt{1^2+\left(-2\right)^2}}=\dfrac{1}{\sqrt{10}}\)
\(\Rightarrow cos\widehat{MCB}=cos\widehat{HBC}=\dfrac{1}{\sqrt{10}}=\dfrac{\left|a+b\right|}{\sqrt{a^2+b^2}.\sqrt{1^2+1^2}}\)
\(\Leftrightarrow\sqrt{a^2+b^2}=\sqrt{5}\left|a+b\right|\Leftrightarrow a^2+b^2=5\left(a+b\right)^2\)
\(\Leftrightarrow2a^2+5ab+2b^2=0\Leftrightarrow\left(a+2b\right)\left(2a+b\right)=0\)
Chọn \(\left(a;b\right)=\left[{}\begin{matrix}\left(2;-1\right)\\\left(1;-2\right)\end{matrix}\right.\) (trường hợp (1;-2) loại do song song BH)
\(\Rightarrow\) Phương trình đường cao kẻ từ C:
\(2\left(x-2\right)-1\left(y-1\right)=0\Leftrightarrow2x-y-3=0\)
Tọa độ C là nghiệm: \(\left\{{}\begin{matrix}x+y+1=0\\2x-y-3=0\end{matrix}\right.\) \(\Rightarrow C\left(...\right)\)
Gọi N là trung điểm BC \(\Rightarrow\) tọa độ N
Tam giác ABC cân tại A \(\Rightarrow\) AN là trung tuyến đồng thời là đường cao
\(\Rightarrow\) Đường thẳng AN vuông góc BC \(\Rightarrow\) nhận (1;-1) là 1 vtpt và đi qua N
\(\Rightarrow\) Phương trình AN
Đường thẳng AB vuông góc CM nên nhận (1;2) là 1 vtpt
\(\Rightarrow\) Phương trình AB (đi qua B và biết vtpt)
\(\Rightarrow\) Tọa độ A là giao điểm AB và AN

a: Tọa độ trung điểm của AC là:
\(\left\{{}\begin{matrix}x=\dfrac{6+2}{2}=\dfrac{8}{2}=4\\y=\dfrac{1+5}{2}=\dfrac{6}{2}=3\end{matrix}\right.\)
b: A(6;1); B(-1;2); C(2;5)
\(\overrightarrow{AB}=\left(-7;1\right);\overrightarrow{AC}=\left(-4;4\right)\)
Vì \(\dfrac{-7}{-4}\ne\dfrac{1}{4}\)
nên A,B,C không thẳng hàng
=>A,B,C lập được thành 1 tam giác
c: Tọa độ trọng tâm của ΔABC là:
\(\left\{{}\begin{matrix}x=\dfrac{6-1+2}{3}=\dfrac{7}{3}\\y=\dfrac{1+2+5}{3}=\dfrac{8}{3}\end{matrix}\right.\)
d: \(AB=\sqrt{\left(-1-6\right)^2+\left(2-1\right)^2}=\sqrt{7^2+1^2}=5\sqrt{2}\)
\(AC=\sqrt{\left(2-6\right)^2+\left(5-1\right)^2}=\sqrt{4^2+4^2}=4\sqrt{2}\)
\(BC=\sqrt{\left(2+1\right)^2+\left(5-2\right)^2}=3\sqrt{2}\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+BC+AC=5\sqrt{2}+4\sqrt{2}+3\sqrt{2}=12\sqrt{2}\)
Xét ΔABC có \(AB^2=BC^2+CA^2\)
nên ΔACB vuông tại C
=>\(S_{CAB}=\dfrac{1}{2}\cdot CA\cdot CB=\dfrac{1}{2}\cdot3\sqrt{2}\cdot4\sqrt{2}=2\sqrt{2}\cdot3\sqrt{2}=12\)

a) Ta có: \(\overrightarrow {BA} = (2 - ( - 2);1 - 5) = (4; - 4)\) và \(\overrightarrow {BC} = ( - 5 - ( - 2);2 - 5) = ( - 3; - 3)\)
b)
Ta có: \(\overrightarrow {BA} .\overrightarrow {BC} = 4.( - 3) + ( - 4).( - 3) = 0\)
\( \Rightarrow \overrightarrow {BA} \bot \overrightarrow {BC} \) hay \(\widehat {ABC} = {90^o}\)
Vậy tam giác ABC vuông tại B.
Lại có: \(AB = \left| {\overrightarrow {BA} } \right| = \sqrt {{4^2} + {{( - 4)}^2}} = 4\sqrt 2 \); \(BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{3^2} + {{( - 3)}^2}} = 3\sqrt 2 \)
Và \(AC = \sqrt {A{B^2} + B{C^2}} = 5\sqrt 2 \) (do \(\Delta ABC\)vuông tại B).
Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}.AB.BC = \frac{1}{2}.4\sqrt 2 .3\sqrt 2 = 12\)
Chu vi tam giác ABC là: \(AB + BC + AC = 4\sqrt 2 + 3\sqrt 2 + 5\sqrt 2 = 12\sqrt 2 \)
c) Tọa độ của trọng tâm G là \(\left( {\frac{{2 + ( - 2) + ( - 5)}}{3};\frac{{1 + 5 + 2}}{3}} \right) = \left( {\frac{{ - 5}}{3};\frac{8}{3}} \right)\)
d) Giả sử điểm D thỏa mãn BCAD là một hình bình hành có tọa độ là (a; b).

Ta có: \(\overrightarrow {CB} = ( 3; 3)\) và \(\overrightarrow {AD} = (a - 2;b - 1)\)
Vì BCAD là một hình bình hành nên \(\overrightarrow {AD} = \overrightarrow {CB} \)
\(\begin{array}{l} \Leftrightarrow (a - 2;b - 1) = ( 3;3)\\ \Leftrightarrow \left\{ \begin{array}{l}a - 2 = 3\\b - 1 = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 5 \\b = 4\end{array} \right.\end{array}\)
Vậy D có tọa độ (5; 4)