Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi số em thích chơi cờ vua là a
số em thích chơi bóng bàn là b
số em thích chơi cả cờ vua và bóng bàn là c
ta có a+b+c=100
và 85=a+c ; 75=b+c
nên 160=a+b+c+c=100+c suy ra c=60 từ đó ta có a=25 . b=15
Số em thích chơi cả hai môn là:
( 100 - 85 ) + ( 100 - 75 ) = 40 (em)
Đáp số: 40 em

gọi số em thích chơi cờ vua là a
số em thích chơi bóng bàn là b
số em thích chơi cả cờ vua và bóng bàn là c
ta có a+b+c=100
và 85=a+c ; 75=b+c
nên 160=a+b+c+c=100+c suy ra c=60 từ đó ta có a=25 . b=15

Tham khảo:
a. Trong 20 lần chơi có 15 lần em thắng, 5 lần bạn em thắng;
b. Xác suất thực nghiệm của sự kiện Em thắng là:\(\frac{{15}}{{20}}=\frac{{3}}{{4}}\)
Xác suất thực nghiệm của sự kiện Bạn em thắng là: \(\frac{{5}}{{20}}=\frac{{1}}{{4}}\)
c. Biểu đồ cột:
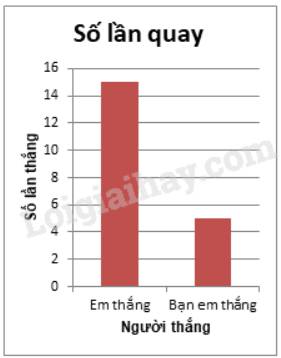

Số em thích chơi cả 2 môn là:
85+75-100=60 (em)
Vậy có 60 em thích chơi cả 2 môn.

Hướng dẫn giải:
Ta giải bài toán bằng cách đi ngược từ dưới lên. Vì tổng số kẹo là 25 nên nếu cuối cùng một người bốc được số lẻ viên kẹo sẽ thua, do người kia sẽ bốc được một số chẵn viên kẹo.
Ta ký hiệu mỗi trạng thái đến lượt An hay Bình đi bằng hai tham số (CL, k), trong đó CL là tính chẵn lẻ của số kẹo mà người chơi đang có, k là số kẹo còn lại trên bàn. Ta viết f(CL, k) = 1 nếu người đi có chiến thuật thắng từ trạng thái này. Trong trường hợp ngược lại f(CL, k) = 0. Mục đích của chúng ta là cần tính F(C, 25). Nếu giá trị này bằng 1 thì An thắng, ngược lại nếu giá trị này bằng 0 thì Bình thắng.
Ví dụ f(C, 1) = 0 vì người đi đang có số chẵn viên kẹo và bắt buộc phải bốc viên kẹo cuối cùng, kết thúc cuộc chơi. f(C, 2) = 1 vì người đi đang có số chẵn viên kẹo và có thể bốc 2 viên kẹo cuối cùng để giành chiến thắng. Cũng như vậy f(C, 3) = 1 (bốc 2). Tương tự như thế thì f(L, 1) = 1 (bốc 1), F(L, 2) = 1 (bốc 1), F(L, 3) = 1 (bốc 3).
Để tính f(C, 4) ta để ý rằng lúc này đối thủ đang có số lẻ viên kẹo. Nếu ta bốc 1, 2 hoặc 3 viên thì sẽ đưa đối thủ đến các trạng thái (L, 3), (L, 2), (L, 1) tương ứng, và đều là các trạng thái thắng của đối thủ. Suy ra f(C, 4) = 0. Với f(L, 4) ta bốc 3 viên, đưa đối thủ vào trạng thái thua (C, 1) và giành chiến thắng.
Tiếp tục, để tính f(C, 5) ta để ý rằng lúc này đối thủ đang có số chẵn viên kẹo. Do đó ta bốc 1 viên và đưa đối thủ vào trạng thái (C, 4) là trạng thái thua, như vậy f(C,5) = 1. Ngược lại từ (L, 5) ta chỉ có thể đưa về (L, 4), (L, 3), (L, 2) là các trạng thái thắng, suy ra f(L, 5) = 0.
Nói tóm lại, một trạng thái là thua nếu mọi cách đi đều đưa về trạng tháng thắng (cho đối thủ), một trạng thái là thắng nếu có một cách đi đưa về trạng thái thua (cho đối thủ). Bằng lý luận này, ta lập được bảng giá trị sau.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| C | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| L | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
| C | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| L | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | |||
| C | 1 | 0 | 1 | 1 | 1 | 1 | 0 | ||
| L | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
Như vậy f(C, 25) = 0, tức là Bình có chiến thuật thắng.
(Đây là bài toán khá khó trong lý thuyết thuật toán và trò chơi).
Ta giải bài toán bằng cách đi ngược từ dưới lên. Vì tổng số kẹo là 25 nên nếu cuối cùng một người bốc được số lẻ viên kẹo sẽ thua, do người kia sẽ bốc được một số chẵn viên kẹo.
Ta ký hiệu mỗi trạng thái đến lượt An hay Bình đi bằng hai tham số (CL, k), trong đó CL là tính chẵn lẻ của số kẹo mà người chơi đang có, k là số kẹo còn lại trên bàn. Ta viết f(CL, k) = 1 nếu người đi có chiến thuật thắng từ trạng thái này. Trong trường hợp ngược lại f(CL, k) = 0. Mục đích của chúng ta là cần tính F(C, 25). Nếu giá trị này bằng 1 thì An thắng, ngược lại nếu giá trị này bằng 0 thì Bình thắng.
Ví dụ f(C, 1) = 0 vì người đi đang có số chẵn viên kẹo và bắt buộc phải bốc viên kẹo cuối cùng, kết thúc cuộc chơi. f(C, 2) = 1 vì người đi đang có số chẵn viên kẹo và có thể bốc 2 viên kẹo cuối cùng để giành chiến thắng. Cũng như vậy f(C, 3) = 1 (bốc 2). Tương tự như thế thì f(L, 1) = 1 (bốc 1), F(L, 2) = 1 (bốc 1), F(L, 3) = 1 (bốc 3).
Để tính f(C, 4) ta để ý rằng lúc này đối thủ đang có số lẻ viên kẹo. Nếu ta bốc 1, 2 hoặc 3 viên thì sẽ đưa đối thủ đến các trạng thái (L, 3), (L, 2), (L, 1) tương ứng, và đều là các trạng thái thắng của đối thủ. Suy ra f(C, 4) = 0. Với f(L, 4) ta bốc 3 viên, đưa đối thủ vào trạng thái thua (C, 1) và giành chiến thắng.
Tiếp tục, để tính f(C, 5) ta để ý rằng lúc này đối thủ đang có số chẵn viên kẹo. Do đó ta bốc 1 viên và đưa đối thủ vào trạng thái (C, 4) là trạng thái thua, như vậy f(C,5) = 1. Ngược lại từ (L, 5) ta chỉ có thể đưa về (L, 4), (L, 3), (L, 2) là các trạng thái thắng, suy ra f(L, 5) = 0.
Nói tóm lại, một trạng thái là thua nếu mọi cách đi đều đưa về trạng tháng thắng (cho đối thủ), một trạng thái là thắng nếu có một cách đi đưa về trạng thái thua (cho đối thủ). Bằng lý luận này, ta lập được bảng giá trị sau.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| C | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| L | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
| C | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| L | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | |||
| C | 1 | 0 | 1 | 1 | 1 | 1 | 0 | ||
| L | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
Như vậy f(C, 25) = 0, tức là Bình có chiến thuật thắng.
(Đây là bài toán khá khó trong lý thuyết thuật toán và trò chơi).
Mình không hiểu câu hỏi lắm nhưng nếu ý thật của nó là mỗi trận bao nhiêu phút thì theo mình là 9 phút
18phút