Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

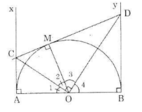
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
OC là tia phân giác của ∠AOM
OD và tia phân giác của ∠BOM
OC và OD là các tia phân giác của hai góc kề bù ∠AOM và ∠BOM nên OC ⊥ OD.
=> ∠COD = 90o (đpcm)
b) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = AC, DM = BC
Do đó: CD = CM + DM = AC + BD (đpcm)
c) Ta có: AC = CM, BD = DM nên AC.BD = CM.MD
ΔCOD vuông tại O, ta có:
CM.MD = OM2 = R2 (R là bán kính đường tròn O).
Vậy AC.BD = R2 (không đổi).

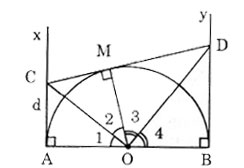 a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = CA; DM = DB;
∠O1 = ∠O2; ∠O3 = ∠O4
⇒ ∠O2 + ∠O3 = ∠O1 + ∠O4 = 1800/2 = 900 (tính chất hai tia phân giác của hai góc kề bù).
⇒ ∠OCD = 900
b) CM và CA là hai tiếp tuyến của đường tròn, cắt nhau tại C nên CM = CA
Tương tự:
DM = DB
⇒ CM + DM = CA + DB
⇒ CD = AC + BD.
c) Ta có OM ⊥ CD
Trong tam giá vuông COD, OM Là đường cao thuộc cạnh huyển
OM2 = CM.DM
Mà OM = OA = OA = AB/2 và CM = AC; DM = BD
Suy ra AC.BD = AB2/2 = không đổi

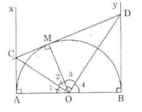
Ta có: AC = CM, BD = DM nên AC.BD = CM.MD
ΔCOD vuông tại O, ta có:
CM.MD = OM2 = R2 (R là bán kính đường tròn O).
Vậy AC.BD = R2 (không đổi).

Bài 1:
a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = CA; DM = DB;
∠O1 = ∠O2; ∠O3 = ∠O4
⇒ ∠O2 + ∠O3 = ∠O1 + ∠O4 = 1800/2 = 900 (tính chất hai tia phân giác của hai góc kề bù).
⇒ ∠OCD = 900
b) CM và CA là hai tiếp tuyến của đường tròn, cắt nhau tại C nên CM = CA
Tương tự:
DM = DB
⇒ CM + DM = CA + DB
⇒ CD = AC + BD.
c) Ta có OM ⊥ CD
Trong tam giá vuông COD, OM Là đường cao thuộc cạnh huyển
OM2 = CM.DM
Mà OM = OA = OA = AB/2 và CM = AC; DM = BD
Suy ra AC.BD = AB2/2 = không đổi

Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = AC, DM = BC
Do đó: CD = CM + DM = AC + BD (đpcm)

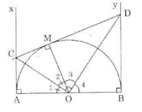
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
OC là tia phân giác của ∠AOM
OD và tia phân giác của ∠BOM
OC và OD là các tia phân giác của hai góc kề bù ∠AOM và ∠BOM nên OC ⊥ OD.
=> ∠COD = 90o (đpcm)

a: Xét (O) co
CM,CA là tiếp tuyên
=>CM=CA
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB
CD=CM+MD
=>CD=CA+BD
b: Xet ΔACN và ΔDBN có
góc NAC=góc NDB
góc ANC=góc DNB
=>ΔACN đồng dạng vơi ΔDBN
=>AC/BD=AN/DN
=>CN/MD=AN/ND
=>MN//AC//BD
a) OCOC và ODOD là các tia phân giác của hai góc kề bù \widehat{AOM}AOM, \widehat{BOM}BOM nên OC \perp ODOC⊥OD.
Vậy \widehat{COD}=90^{\circ}COD=90∘.
b) Theo tính chất của hai tiếp tuyến cắt nhau, ta có: CM=AC, DM=BDCM=AC,DM=BD
Do đó CD=CM+DM=AC+BDCD=CM+DM=AC+BD.
c) Ta có: AC.BD=CM.MDAC.BD=CM.MD
Xét tam giác CODCOD vuông tại OO và OM \perp CDOM⊥CD nên ta có
CM. MD=OM^{2}=R^{2}CM.MD=OM2=R2 (RR là bán kính của đường tròn OO).
Vậy AC.BD=R^2AC.BD=R2 (không đổi).