Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(\sqrt{\frac{2a}{3}}.\sqrt{\frac{3a}{8}}=\sqrt{\frac{6a^2}{24}}=\sqrt{\frac{a^2}{4}}=\left|\frac{a}{2}\right|=\frac{a}{2}\)
do \(a\ge0\)
b, \(\sqrt{13a}.\sqrt{\frac{52}{a}}=\sqrt{\frac{676a}{a}}=\sqrt{676}=26\)
c, \(\sqrt{5a}.\sqrt{45a}-3a=\sqrt{225a^2}-3a=\left|15a\right|-3a\)
\(=15a-3a=12a\)do a > 0
d, \(=\left(3-a\right)^2-\sqrt{0,2}.\sqrt{180a^2}\)
\(=\left(3-a\right)^2-\sqrt{36a^2}=\left(3-a\right)^2-\left|6a\right|\)
Với \(a\ge0\Rightarrow\left(3-a\right)^2-6a=a^2-6a+9-6a=a^2-12a+9\)
Với \(a< 0\Rightarrow\left(3-a\right)^2+6a=a^2-6a+9+6a=a^2+9\)

(Vì x > 0 nên |x| = x; y2 > 0 với mọi y ≠ 0)
(Vì x2 ≥ 0 với mọi x; và vì y < 0 nên |2y| = – 2y)
(Vì x < 0 nên |5x| = – 5x; y > 0 nên |y3| = y3)
(Vì x2y4 = (xy2)2 > 0 với mọi x ≠ 0, y ≠ 0)

a, \(2\sqrt{a^2}-5a=2\left|a\right|-5a\)do a < 0
\(=-2a-5a=-7a\)
b, \(\sqrt{25a^2}+3a=\sqrt{\left(5a\right)^2}+3a=\left|5a\right|+3a\)do \(a\le0\)
TH1 : \(-5a+3a=-2a\)với \(a< 0\)
hoặc TH2 : \(5+3=8\)
c, \(\sqrt{9a^4}+3a^2=\sqrt{\left(3a^2\right)^2}+3a^2=\left|3a^2\right|+3a^2\)
\(=3a^2+3a^2=6a^2\)do \(3>0;a^2\ge0\forall a\Rightarrow3a^2\ge0\forall a\)
d, \(5\sqrt{4a^6}-3a^3=5\sqrt{\left(2a^3\right)^2}-3a^3\)
\(=5\left|2a^3\right|-3a^3=-10a^3-3a^3=-13a^3\)do \(a< 0\Rightarrow a^3< 0\)
a) \(2\sqrt{a^2}-5a\)=2\(|a|\)-5a = -2a-5a=-7a
b) \(\sqrt{25a^2}\) +3a = 5\(|a|\) + 3a=5a+3a=8a.
c) \(\sqrt{9a^4}\) + 3\(a^2\)=6\(a^2\)
d) \(5\sqrt{4a^6}\) - 3\(a^3\)=-13\(a^3\)

a, Ta có \(\sqrt{25-16}=\sqrt{9}=3\)
\(\sqrt{25}-\sqrt{16}=5-4=1\)
Do 3 > 1 nên \(\sqrt{25-16}>\sqrt{25}-\sqrt{16}\)
a) căn 25 - 16 > căn 25 - căn 16
b)Với a>b>0a>b>0 nên \sqrt{a},\sqrt{b},\sqrt{a-b}a,b,− đều xác định
Để so sánh \sqrt{a}-\sqrt{b}a−b và \sqrt{a-b}− ta quy về so sánh \sqrt{a}a và \sqrt{a-b}+\sqrt{b}−+b.
+) (\sqrt{a})^2=a(a)2=a.
+) (\sqrt{a-b}+\sqrt{b})^2=(\sqrt{a-b})^2+2\sqrt{a-b}.\sqrt{b}+(\sqrt{b})^2=a-b+b+2\sqrt{a-b}.\sqrt{b}=a+2\sqrt{a-b}.\sqrt{b}(−+b)2=(−)2+2−.b+(b)2=a−b+b+2−.b=a+2−
.b.
Do a>b>0a>b>0 nên 2\sqrt{a-b}.\sqrt{b}>02−.b>0
\Rightarrow⇒ a+2\sqrt{a-b}.\sqrt{b}>aa+2−.b>a
\Rightarrow⇒ (\sqrt{a-b}+\sqrt{b})^2>(\sqrt{a})^2(−+b)2>(a)2
Do \sqrt{a},\sqrt{a-b}+\sqrt{b}>0a,−+b>0
\Rightarrow⇒ \sqrt{a-b}+\sqrt{b}>\sqrt{a}−+b>a
\Leftrightarrow⇔ \sqrt{a-b}>\sqrt{a}-\sqrt{b}−>a−b (đpcm)
Vậy \sqrt{a-b}>\sqrt{a}-\sqrt{b}−>a−b.

bạn tham khảo nha : https://loigiaihay.com/bai-76-trang-41-sgk-toan-9-tap-1-c44a26988.html

a) Ta có : Vì \(x\ge0\)và \(y\ge0\)nên \(x+y\ge0\)\(\Leftrightarrow\left|x+y\right|=x+y\)
\(\frac{2}{x^2-y^2}\sqrt{\frac{3\left(x+y\right)^2}{2}}\)
\(=\frac{2}{x^2-y^2}\sqrt{\frac{3}{2}.\left(x+y\right)^2}\)
\(=\frac{2}{x^2-y^2}.\sqrt{\frac{3}{2}}.\left|x+y\right|\)
\(=\frac{2}{\left(x-y\right)\left(x+y\right)}.\sqrt{\frac{3}{2}}.\left(x+y\right)\)
\(=\frac{2}{x-y}.\sqrt{\frac{3}{2}}\)
\(=\frac{1}{x-y}.2.\sqrt{\frac{3}{2}}\)
\(=\frac{1}{x-y}.\sqrt{\frac{2^2.3}{2}}\)
\(=\frac{1}{x-y}.\sqrt{6}=\frac{\sqrt{6}}{x-y}\)
a, \(\frac{2}{x^2-y^2}\sqrt{\frac{3\left(x+y\right)^2}{2}}=\frac{2}{x^2-y^2}\frac{\sqrt{3}\left|x+y\right|}{\sqrt{2}}=\frac{2\sqrt{3}\left(x+y\right)}{\left(x-y\right)\left(x+y\right)\sqrt{2}}\)
do \(x\ge0;y\ge0\)
\(=\frac{2\sqrt{3}}{\sqrt{2}\left(x-y\right)}=\frac{2\sqrt{6}}{2\left(x-y\right)}=\frac{\sqrt{6}}{x-y}\)

a) ab2.√3a2b4=ab2.√3√a2b4ab2.3a2b4=ab2.3a2b4
=ab2.√3√a2.√b4=ab2.√3|a|.|b2|=ab2.3a2.b4=ab2.3|a|.|b2|
=ab2.√3(−a).b2=ab2.3(−a).b2 (Do a<0a<0 nên |a|=−a|a|=−a và b≠0b≠0 nên b2>0b2>0 ⇒⇒ ∣∣b2∣∣=b2|b2|=b2)
=−√3=−3.
b) √27(a−3)248=√9(a−3)21627(a−3)248=9(a−3)216
=√9.√(a−3)2√16=3.|a−3|4=9.(a−3)216=3.|a−3|4
=3(a−3)4=3(a−3)4.
(Do a>3a>3 nên |a−3|=a−3|a−3|=a−3)
c) √9+12a+4a2b2=√32+2.3.2a+(2a)2√b29+12a+4a2b2=32+2.3.2a+(2a)2b2
=√(3+2a)2√b2=|3+2a||b|=(3+2a)2b2=|3+2a||b|
=3+2a−b=−2a+3b=3+2a−b=−2a+3b.
(Do a≥−1,5a≥−1,5 ⇒⇒ 3+2a≥03+2a≥0 nên |3+2a|=3+2a|3+2a|=3+2a và b<0b<0 nên |b|=−b|b|=−b)
d) (a−b).√ab(a−b)2=(a−b).√ab√(a−b)2(a−b).ab(a−b)2=(a−b).ab(a−b)2
=(a−b).√ab|a−b|=(a−b).√ab−(a−b)=(a−b).ab|a−b|=(a−b).ab−(a−b)
=−√ab=−ab.
(Do a<b<0a<b<0 nên |a−b|=−(a−b)|a−b|=−(a−b) và ab>0ab>0)
a) ab2.√3a2b4=ab2.√3√a2b4ab2.3a2b4=ab2.3a2b4
=ab2.√3√a2.√b4=ab2.√3|a|.|b2|=ab2.3a2.b4=ab2.3|a|.|b2|
=ab2.√3(−a).b2=ab2.3(−a).b2 (Do a<0a<0 nên |a|=−a|a|=−a và b≠0b≠0 nên b2>0b2>0 ⇒⇒ ∣∣b2∣∣=b2|b2|=b2)
=−√3=−3.
b) √27(a−3)248=√9(a−3)21627(a−3)248=9(a−3)216
=√9.√(a−3)2√16=3.|a−3|4=9.(a−3)216=3.|a−3|4
=3(a−3)4=3(a−3)4.
(Do a>3a>3 nên |a−3|=a−3|a−3|=a−3)
c) √9+12a+4a2b2=√32+2.3.2a+(2a)2√b29+12a+4a2b2=32+2.3.2a+(2a)2b2
=√(3+2a)2√b2=|3+2a||b|=(3+2a)2b2=|3+2a||b|
=3+2a−b=−2a+3b=3+2a−b=−2a+3b.
(Do a≥−1,5a≥−1,5 ⇒⇒ 3+2a≥03+2a≥0 nên |3+2a|=3+2a|3+2a|=3+2a và b<0b<0 nên |b|=−b|b|=−b)
d) (a−b).√ab(a−b)2=(a−b).√ab√(a−b)2(a−b).ab(a−b)2=(a−b).ab(a−b)2
=(a−b).√ab|a−b|=(a−b).√ab−(a−b)=(a−b).ab|a−b|=(a−b).ab−(a−b)
=−√ab=−ab.
(Do a<b<0a<b<0 nên |a−b|=−(a−b)|a−b|=−(a−b) và ab>0ab>0)

LG a
√18(√2−√3)2;18(2−3)2;
Phương pháp giải:
+ √ab=√a.√bab=a.b, với a, b≥0a, b≥0.
+ |a|=a|a|=a, nếu a≥0a≥0
|a|=−a|a|=−a nếu a<0a<0.
+ Sử dụng định lí so sánh hai căn bậc hai số học: Với hai số a, ba, b không âm, ta có:
a<b⇔√a<√ba<b⇔a<b
Lời giải chi tiết:
Ta có:
√18(√2−√3)2=√18.√(√2−√3)218(2−3)2=18.(2−3)2
=√9.2.|√2−√3|=√32.2.|√2−√3|=9.2.|2−3|=32.2.|2−3|
=3√2.|√2−√3|=3√2(√3−√2)=32.|2−3|=32(3−2)
=3√2.3−3(√2)2=32.3−3(2)2
=3√6−3.2=3√6−6=36−3.2=36−6.
(Vì 2<3⇔√2<√3⇔√2−√3<02<3⇔2<3⇔2−3<0
Do đó: |√2−√3|=−(√2−√3)=−√2+√3|2−3|=−(2−3)=−2+3=√3−√2=3−2).
LG b
ab√1+1a2b2ab1+1a2b2
Phương pháp giải:
+ √ab=√a.√bab=a.b, với a, b≥0a, b≥0.
+ √ab=√a√bab=ab, với a≥0, b>0a≥0, b>0.
+ |a|=a|a|=a, nếu a≥0a≥0
|a|=−a|a|=−a nếu a<0a<0.
Lời giải chi tiết:
Ta có:
ab√1+1a2b2=ab√a2b2a2b2+1a2b2=ab√a2b2+1a2b2ab1+1a2b2=aba2b2a2b2+1a2b2=aba2b2+1a2b2
=ab√a2b2+1√a2b2=ab√a2b2+1√(ab)2=aba2b2+1a2b2=aba2b2+1(ab)2
=ab√a2b2+1|ab|=aba2b2+1|ab|
Nếu ab>0ab>0 thì |ab|=ab|ab|=ab
⇒ab√a2b2+1|ab|=ab√a2b2+1ab=√a2b2+1⇒aba2b2+1|ab|=aba2b2+1ab=a2b2+1.
Nếu ab<0ab<0 thì |ab|=−ab|ab|=−ab
⇒ab√a2b2+1|ab|=ab√a2b2+1−ab=−√a2b2+1⇒aba2b2+1|ab|=aba2b2+1−ab=−a2b2+1.
LG c
√ab3+ab4ab3+ab4
Phương pháp giải:
+ √ab=√a.√bab=a.b, với a, b≥0a, b≥0.
+ √ab=√a√bab=ab, với a≥0, b>0a≥0, b>0.
+ |a|=a|a|=a, nếu a≥0a≥0
|a|=−a|a|=−a nếu a<0a<0.
Lời giải chi tiết:
Ta có:
√ab3+ab4=√a.bb3.b+ab4=√abb4+ab4ab3+ab4=a.bb3.b+ab4=abb4+ab4
=√ab+ab4=√ab+a√(b2)2=√ab+a|b2|=√ab+ab2=ab+ab4=ab+a(b2)2=ab+a|b2|=ab+ab2.
(Vì b2>0b2>0 với mọi b≠0b≠0 nên |b2|=b2|b2|=b2).
LG d
a+√ab√a+√ba+aba+b
Phương pháp giải:
+ √ab=√a.√bab=a.b, với a, b≥0a, b≥0.
+ √ab=√a√bab=ab, với a≥0, b>0a≥0, b>0.
+ |a|=a|a|=a, nếu a≥0a≥0
|a|=−a|a|=−a nếu a<0a<0.
Lời giải chi tiết:
Ta có:
a+√ab√a+√b=(√a)2+√a.√b√a+√b=√a(√a+√b)√a+√ba+aba+b=(a)2+a.ba+b=a(a+b)a+b
=√a=a.
Cách khác:
a+√ab√a+√b=(a+√ab)(√a−√b)(√a+√b)(√a−√b)=a√a−a√b+√ab.√a−√ab.√b(√a)2−(√b)2=a√a−a√b+a√b−b√aa−b=a√a−b√aa−b=√a(a−b)a−b=√a
a) 2√3.(√3−√2)=6−2√6.23.(3−2)=6−26.
b) ab|ab|√1+a2 b2ab|ab|1+a2 b2. Rút gọn hơn, ta có kết quả
+) ab>0ab>0 thì ab√1+1a2b2=√1+a2 b2ab1+1a2b2=1+a2 b2.
+) ab<0ab<0 thì ab√1+1a2b2=−√1+a2 b2ab1+1a2b2=−1+a2 b2.
c) 1b2√ab+a1b2ab+a.
d) Cách 1.
a+√ab√a+√b=(a+√ab)(√a−√b)(√a+√b)(√a−√b)a+aba+b=(a+ab)(a−b)(a+b)(a−b).
=a√a+√a2 b−a√b−√ab2a−b=√a(a−b)a−b=√a

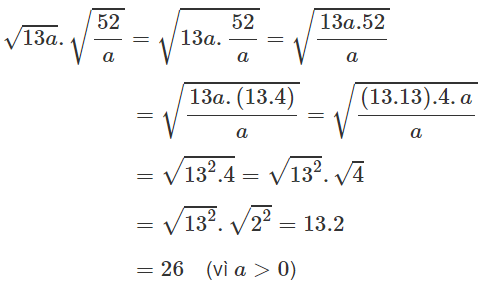

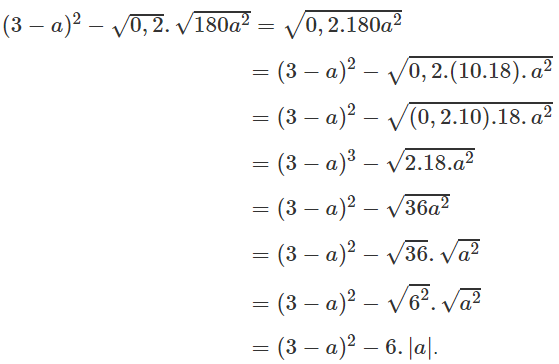
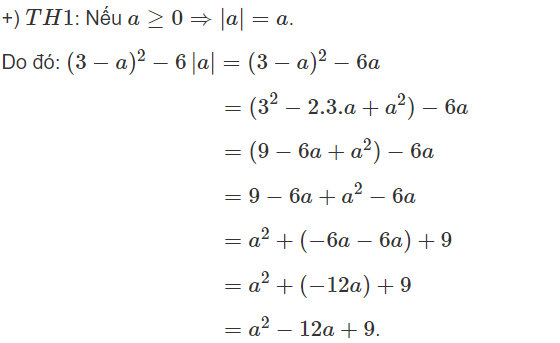
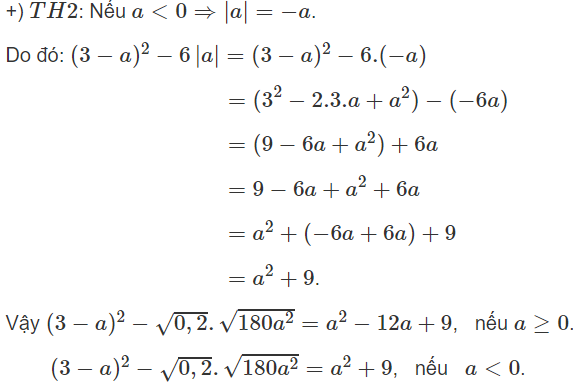
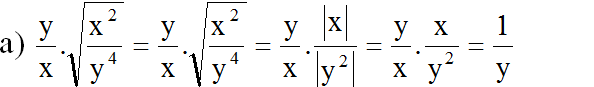
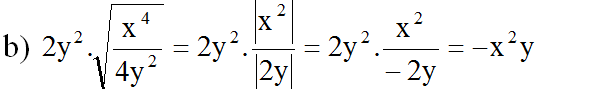
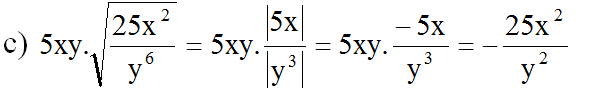
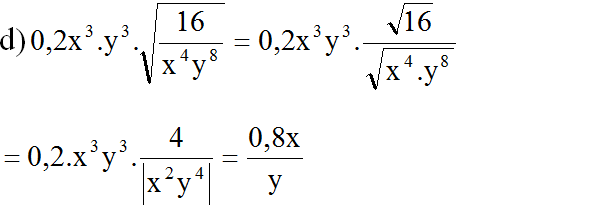
Bạn học tốt nhé
a)0,6.a
b)\(a^2\).(a-3)
c)36.(a-1)
d)\(\dfrac{1.a^2}{a-b}\).(a-b)