Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ví dụ: phương trình (1) x - 1 = 3 có tập nghiệm S1 = {4}.
Nhân hai vế của phương trình (1) với x, ta được phương trình:
(x - 1)x = 3x (2)
⇔ (x - 1)x - 3x = 0
⇔ x(x - 4) = 0
Phương trình (2) có tập nghiệm là S2 = {0, 4}.
Vì S1 ≠ S2 nên hai phương trình (1) và (2) không tương đương.
3. Với điều kiện nào của a thì phương trình ax + b = 0 là một phương trình bậc nhất? (a và b là hai hằng số).
Ví dụ: phương trình (1) x - 1 = 3 có tập nghiệm S1 = {4}.
Nhân hai vế của phương trình (1) với x, ta được phương trình:
(x - 1)x = 3x (2)
⇔ (x - 1)x - 3x = 0
⇔ x(x - 4) = 0
Phương trình (2) có tập nghiệm là S2 = {0, 4}.
Vì S1 ≠ S2 nên hai phương trình (1) và (2) không tương đương.
a) Phương trình bậc nhất một ẩn là phương trình 2x -8 = 0
b) Hai phương trình tương đương là hai phương trình có cùng tập nghiệm
Hai PT đã cho tương đương với nhau vì chúng có cùng tập nghiệm
S = {-2/3}
a) Phương trình bậc nhất một ẩn là phương trình :
2x - 8 = 0
b) Hai phương trình tương đương với nhau vì chúng có cùng tập nghiệm
Hai PT đã cho tương đương với nhau vì chúng có cùng tập nghiệm
S = ( -2 / 3 )
ai tk mk mk tk lại!!
Khẳng định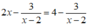 
và 2x = 4 là hai phương trình tương đương là sai.
Vì phương trình 2x = 4 có nghiệm x = 2. Nhưng với x = 2 thì phân thức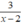 
vô nghĩa.
Vậy x = 2 không là nghiệm của phương trình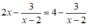 
.
Khi biến đổi phương trình mà làm mất mẫu chứa ẩn của phương trình thì phương trình nhận được:
A . luôn không tương đương với phương trình ban đầu
B . có thể không tương đương với phương trình ban đầu
C. luôn tương đương với phương trình ban đầu
a)sai
b)đúng