Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nối NA, NB. Gọi D là giao điểm của NA với đường thẳng d, nối DB
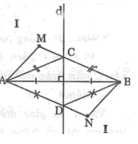
Ta có: NA = ND + DA
Mà DA = DB (tính chất đường trung trực)
Suy ra: NA = ND + DB (3)
Trong ΔNDB, ta có: NB < ND + DB
(bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra: NA > NB.

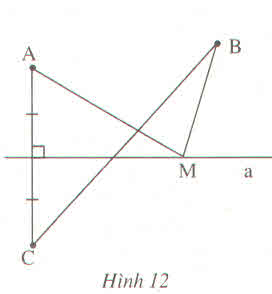
Nối MA, MB
Gọi C là giao điểm của MB với đường thẳng d, nối CA
Ta có: MB = MC + CB
Mà CA = CB (tính chất đường trung trực)
Suy ra: MB = MC + CA (1)
Trong ΔMAC, ta có:
MA < MC + CA (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra: MA < MB

a. Gọi C là giao điểm của MB với đường thẳng d.
Ta có: MB=MC+CB
mà CA=CB(tính chất đường trung trực)
Suy ra: MB=MC+CA(1)
Trong ΔMAC ta có:
MA<MC+CA(bất đẳng thức tam giác)(2)
Từ (1) và (2) suy ra: MA<MB
b.Gọi D là giao điểm của NA với đường thẳng d.
Ta có: NA=ND+DA
mà DA=DB(tính chất đường trung trực)
Suy ra: NA=ND+DB(3)
Trong ΔNDB, ta có:
NB<ND+DB (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra: NA>NB
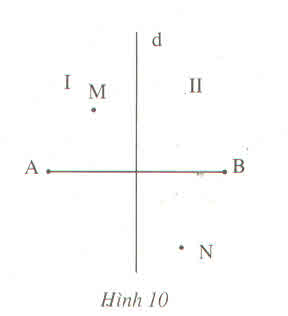
c) Theo phần a và b; với điểm H bất kì ta có:
+ Nếu H nằm trong phần PA thì HA < HB.
+ Nếu H nằm trong phần PB thì HB < HA.
+ Nếu H nằm trên đường thẳng d thì HA = HB (tính chất đường trung trực)
Do đó, để KA < KB thì K nằm trong phần PA.

a: Gọi N là giao điểm của BC với a
Nếu M khác N
Vì M nằm trên đường trung trực của AC
nên MA=MC
XétΔMBC có BC<MB+MC
=>BC<MA+MB
Nếu M trùng với N thì nối NA
Vì N nằm trên đường trung trực của AC nên NA=NC
=>MA+MB=NA+NB=BC
=>MA+MB>=BC
b: MA+MB nhỏ nhất khi M là giao điểm của BC với a

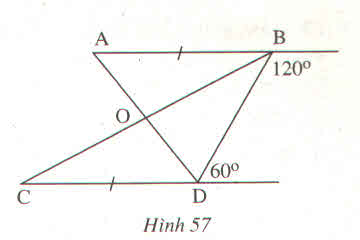
Ta có: góc B + góc D = 1200 + 600 = 1800
Mà hai góc này TCP
=> AB // CD
Xét tam giác ABO và tam giác CDO có:
AB = CD (GT)
ABC = BCD (AB // CD)
BAD = ADC (AB // CD)
=> tam giác ABO = tam giác CDO
=> AO = OD
=> O là trung điểm AD
Ta có: tam giác ABO = tam giác CDO
=> BO = OC
=> O là trung điểm BC

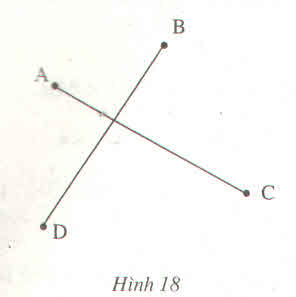
Nếu M không là giao điểm của AC và BD thì MA+MC>AC; MB+MD>BD
=>MA+MB+MC+MD>AC+BD(1)
Nếu M là giao điểm của AC và BD thì MA+MB+MC+MD=AC+BD(2)
Từ (1) và (2) suy ra MA+MB+MC+MD>=AC+BD
Dấu '=' xảy ra khi M là giao điểm của AC và BD

Nếp gấp zt vuông góc với đường thẳng xy tại O. Có bốn góc vuông là xOz,yOz,yOt,tOx.

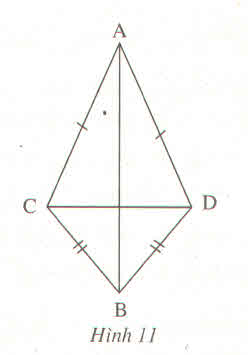
vì AC=AD=>A thuộc đường trung trực của CD
CB=BD=>B thuộc đường trung trực của CD
=>AB thuộc đường trung trực của CD=>AB vuông góc với CD


a: MC+CB=MB
mà CB=CA
nên MC+CA=MB
mà MC+CA<MA
nên MA>MB
b: Gọi D là giao điểm của NA với d
C là giao điểm của CB với d
Ta có:NA=ND+DA
mà DA=DB
nen NA=ND+DB(3)
mà NB<ND+DB
nên NA>NB