Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Giải
Chu vi hình thoi là:
4. 4 = 16 (cm)
Diện tích hình thoi là:
6.4:2 =24:2=12 (cm vuông)
Đáp số: Diện tích : 12 cm vuông
Chu vi : 16 cm

1) Đỉnh: A, B, C, D
Cạnh: AB, BC, CD, DA
Đường chéo: AC, BD
Hai cạnh đối: AB và CD; BC và AD
2) Ta đo được: \(\widehat{A} = 90^0; \widehat{B} = 90^0; \widehat{C} = 90^0; \widehat{D} = 90^0\). Vậy các góc của hình chữ nhật đều bằng nhau và bằng 90o
3) Ta đo được: AB = CD ; AD = BC nên hai cạnh đối của hình chữ nhật bằng nhau
AC = BD nên hai đường chéo của hình chữ nhật bằng nhau.

Vẽ hình vuông cạnh 7 cm bằng thước và êke theo hướng dẫn sau:
- Vẽ đoạn thẳng CD dài 7 cm.
- Vẽ hai đường thẳng vuông góc với CD tại C và D như hình vẽ.
- Trên đường thẳng qua C lấy đoạn thẳng CB = 7cm; trên đường thẳng qua D lấy đoạn thẳng DA = 7 cm.
- Nối hai điểm A và B ta được hình vuông cần vẽ.
- Kẻ hai đường chéo của hình vuông.
- Sử dụng compa đo độ dài của hai đường chéo thấy hai đường chéo bằng nhau.

1) Dùng thước thẳng hoặc compa, ta được: AB = BC = CD = AD. Vậy các cạnh của hình thoi bằng nhau.
2) Dùng eke ta thấy AC vuông góc với BD. Vậy hai đường chéo của hình thoi vuông góc với nhau.
3) + Khi đặt eke vuông góc với AB, ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
+ Khi đặt eke vuông góc với BC, ta thấy eke cũng vuông góc với AD. Do đó BC và AD song song với nhau.
Vậy các cạnh đối của hình thoi song song với nhau.
4) Gấp giấy, ta thấy các góc đối của hình thoi ABCD bằng nhau.

a) Các cạnh của hình thoi bằng nhau.
b) Kẻ đường thẳng qua B và vuông góc với BC. Đặt êke có góc vuông tại điểm cắt nhau giữa đường thẳng vừa kẻ và AD, đặt một cạnh góc vuông của êke trùng với đường thẳng ta thấy cạnh góc vuông còn lại của êke trùng khít với cạnh AD.
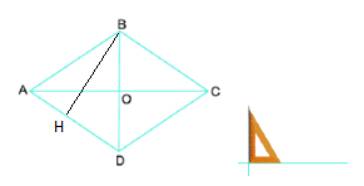
Khi đó BC và AD song song với nhau.
Tương tự AB và CD song song với nhau.
c) Tương tự như phần b, ta đặt đầu có góc vuông tại điểm O, đặt một cạnh góc vuông trùng với OB thì cạnh góc vuông còn lại trùng với OC hoặc OA. Khi đó AC và BD vuông góc với nhau.