Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trình tự dựng gồm 3 bước:
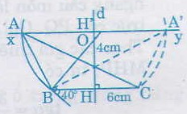
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 40o trên đoạn thẳng BC.
- Dựng đường thẳng xy song song với BC và cách BC một khoảng là 4cm như sau:
Trên đường trung trực d của đoạn thẳng BC lấy đoạn HH' = 4cm (dùng thước có chia khoảng mm). Dựng đường thẳng xy vuông góc với HH' tại H
Gọi giao điểm xy và cung chứa góc là ,
. Khi đó tam giác ABC hoặc A'BC đều thỏa yêu cầu của đề toán
Trình tự dựng gồm 3 bước:
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 40o trên đoạn thẳng BC.
- Dựng đường thẳng xy song song với BC và cách BC một khoảng là 4cm như sau:
Trên đường trung trực d của đoạn thẳng BC lấy đoạn HH' = 4cm (dùng thước có chia khoảng mm). Dựng đường thẳng xy vuông góc với HH' tại H
Gọi giao điểm xy và cung chứa góc là \(\widehat{A}\) , \(\widehat{A'}\). Khi đó tam giác ABC hoặc A'BC đều thỏa yêu cầu của đề toán


Trình tự dựng gồm 3 bước:
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 40o trên đoạn thẳng BC.
- Dựng đường thẳng xy song song với BC và cách BC một khoảng là 4cm như sau:
Trên đường trung trực d của đoạn thẳng BC lấy đoạn HH' = 4cm (dùng thước có chia khoảng mm). Dựng đường thẳng xy vuông góc với HH' tại H
Gọi giao điểm xy và cung chứa góc là ,
. Khi đó tam giác ABC hoặc A'BC đều thỏa yêu cầu của đề toán

Cách dựng:
+ Dựng đoạn thẳng BC = 6cm.
+ Dựng cung chứa góc 40º trên đoạn thẳng BC (tương tự bài 46) :
Dựng tia Bx sao cho 
Dựng tia By ⊥ Bx.
Dựng đường trung trực của BC cắt By tại O.
Dựng đường tròn (O; OB).
Cung lớn BC chính là cung chứa góc 40º dựng trên đoạn BC.
+ Dựng đường thẳng d song song với BC và cách BC một đoạn 4cm:
Lấy D là trung điểm BC.
Trên đường trung trực của BC lấy D’ sao cho DD’ = 4cm.
Dựng đường thẳng d đi qua D’ và vuông góc với DD’.
+ Đường thẳng d cắt cung lớn BC tại A.
Ta được ΔABC cần dựng.
Chứng minh:
+ Theo cách dựng có BC = 6cm.
+ A ∈ cung chứa góc 40º dựng trên đoạn BC

+ A ∈ d song song với BC và cách BC 4cm
⇒ AH = DD’ = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài.
Biện luận: Do d cắt cung lớn BC tại hai điểm nên bài toán có hai nghiệm hình.

a: Xét ΔAHB vuông tại H có sin B=AH/AB
nên AB=5,96(cm)
=>BH=2,52(cm)
Xét ΔAHC vuông tại H có sin C=AH/AC
nên AC=7,05(cm)
=>HC=4,53(cm)
BC=2,52+4,53=7,05(cm)
C=7,05+7,05+5,96=20,06(cm)
b: góc A=180-58-40=82 độ
Xét ΔBHA vuông tại H có tan A=BH/HA
nên HA=0,56(cm)
Xét ΔBHC vuông tại H có tan C=BH/HC
nên HC=4,77(cm)
=>AC=5,33(cm)
\(S_{ABC}=\dfrac{5.33\cdot4}{2}=10.66\left(cm^2\right)\)

\(\widehat{BAC}=60^0\Rightarrow\widehat{BOC}=120^0\)
\(BC=\sqrt{2R^2-2R^2.\cos120^0}=R\sqrt{3}=2\sqrt{3}\left(cm\right)\)
\(S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}.3.2\sqrt{3}=3\sqrt{3}\left(cm^2\right)\)

A B C D E H K O a) Xét tứ giác ADHE có \(\widehat{ADH}+\widehat{AEH}=90^0+90^0=180^0\)
Suy ra tứ giác ADHE nội tiếp
Xét tứ giác BEDC có \(\widehat{BDC}=\widehat{BEC}=90^0\)
Suy ra tứ giác BEDC nội tiếp
b) Ta có tứ giác BEDC nội tiếp\(\Rightarrow\widehat{AED}=\widehat{ACB}\)
Xét △ADE và △ABC có
\(\widehat{AED}=\widehat{ACB}\)(cmt)
\(\widehat{A}\) chung
Suy ra △ADE \(\sim\) △ABC(g-g)\(\Rightarrow\frac{DE}{BC}=\frac{AD}{AB}=cos_{\widehat{BAD}}=cos_{45^0}=\frac{\sqrt{2}}{2}\)
c) Vẽ đường kính AOK
Ta có \(\widehat{AED}=\widehat{ACB}\)\(\Leftrightarrow\)\(\widehat{AED}+\widehat{EAO}=\widehat{ACB}+\widehat{BAK}=\frac{sd\stackrel\frown{AB}}{2}+\frac{sd\stackrel\frown{BK}}{2}=\frac{sd\stackrel\frown{AB}+sd\stackrel\frown{BK}}{2}=\frac{sd\stackrel\frown{AK}}{2}=\frac{180^0}{2}=90^0\Rightarrow\)OA⊥DE
Trình tự dựng gồm các bước sau:
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 80 trên đoạn thẳng BC (cung BmC).
- Trên đường vuông góc với BC tại I(I là trung điểm BC), chọn điểm K sao cho IK = 2cm. Từ K dựng đường thẳng vuông góc với IK. Đường thẳng này cắt cung chứa góc BmC tại A và A'.
ΔABC (hoặc ΔA'BC) là tam giác thỏa mãn yêu cầu đề bài.