Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cos \alpha \) ta có:
\(\cos \alpha = \frac{{ - \sqrt 2 }}{2}\) với \(\alpha = {135^o}\)
b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\sin \alpha \) ta có:
\(\sin \alpha = 0\) với \(\alpha = {0^o}\) và \(\alpha = {180^o}\)
c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\tan \alpha \) ta có:
\(\tan \alpha = 1\) với \(\alpha = {45^o}\)
d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cot \alpha \) ta có:
\(\cot \alpha \) không xác định với \(\alpha = {0^o}\) hoặc \(\alpha = {180^o}\)

a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\sin \alpha \) ta có:
\(\sin \alpha = \frac{{\sqrt 3 }}{2}\) với \(\alpha = {60^o}\) và \(\alpha = {120^o}\)
b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cos \alpha \) ta có:
\(\cos \alpha = \frac{{ - \sqrt 2 }}{2}\) với \(\alpha = {135^o}\)
c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\tan \alpha \) ta có:
\(\tan \alpha = - 1\) với \(\alpha = {135^o}\)
d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cot \alpha \) ta có:
\(\cot \alpha = - \sqrt 3 \) với \(\alpha = {150^o}\)

a)
Trên nửa đường tròn đơn vị, lấy điểm M sao cho \(\widehat {xOM} = \alpha \)
Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.
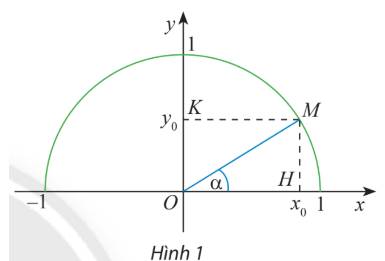
Ta có: tam giác vuông OHM vuông tại H và \(\alpha = \widehat {xOM}\)
Do đó: \(\sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.\)
\( \Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1\)
b) Ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\)
c) Với \(\alpha \ne {90^o}\) ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\)
d) Ta có:
\(\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\)

a) Ta có: \(\left\{ \begin{array}{l}\sin {100^o} = \sin \left( {{{180}^o} - {{80}^o}} \right) = \sin {80^o}\\\cos {164^o} = \cos \left( {{{180}^o} - {{16}^o}} \right) = - \cos {16^o}\end{array} \right.\)
\( \Rightarrow \sin {100^o} + \sin {80^o} + \cos {16^o} + \cos {164^o}\)\( = \sin {80^o} + \sin {80^o} + \cos {16^o}-\cos {16^o}\)\( = 2\sin {80^o}.\)
b)
Ta có:
\(\left\{ \begin{array}{l}\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha \\\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha \\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array} \right.\quad ({0^o} < \alpha < {90^o})\)\( \Rightarrow 2\sin \left( {{{180}^o} - \alpha } \right).\cot \alpha - \cos \left( {{{180}^o} - \alpha } \right).\tan \alpha .\cot \left( {{{180}^o} - \alpha } \right)\) \( = 2\sin \alpha .\cot \alpha - \left( { - \cos \alpha } \right).\tan \alpha .\left( { - \cot \alpha } \right)\)\( = 2\sin \alpha .\cot \alpha - \cos \alpha .\tan \alpha .\cot \alpha \)
\( = 2\sin \alpha .\frac{{\cos \alpha }}{{\sin \alpha }} - \cos \alpha .\left( {\tan \alpha .\cot \alpha } \right)\)\( = 2\cos \alpha - \cos \alpha .1 = \cos \alpha .\)

a)
\(\begin{array}{l}\cos {80^o}43'51'' = 0,161;\\\tan {147^o}12'25'' = - 0,644;\\\cot {99^o}9'19'' = - 0,161\end{array}\)
b) \(\alpha = {136^o}18'9,81''.\)

Tham khảo:
a)
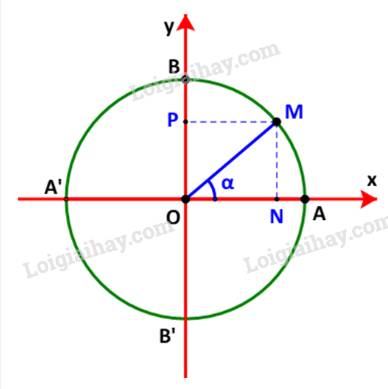
Gọi M(x;y) là điểm trên đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha \). Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
Ta có: \(\left\{ \begin{array}{l}x = \cos \alpha \\y = \sin \alpha \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\cos ^2}\alpha = {x^2}\\{\sin ^2}\alpha = {y^2}\end{array} \right.\)(1)
Mà \(\left\{ \begin{array}{l}\left| x \right| = ON\\\left| y \right| = OP = MN\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} = {\left| x \right|^2} = O{N^2}\\{y^2} = {\left| y \right|^2} = M{N^2}\end{array} \right.\)(2)
Từ (1) và (2) suy ra \({\sin ^2}\alpha + {\cos ^2}\alpha = O{N^2} + M{N^2} = O{M^2}\) (do \(\Delta OMN\) vuông tại N)
\( \Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\) (vì OM =1). (đpcm)
b)
Ta có: \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\;\;(\alpha \ne {90^o})\)
\( \Rightarrow 1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }}\)
Mà theo ý a) ta có \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) với mọi góc \(\alpha \)
\( \Rightarrow 1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\) (đpcm)
c)
Ta có: \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\;\;\;({0^o} < \alpha < {180^o})\)
\( \Rightarrow 1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }}\)
Mà theo ý a) ta có \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) với mọi góc \(\alpha \)
\( \Rightarrow 1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\) (đpcm)

\(P=\dfrac{2sin\alpha-3cos\alpha}{3sin\alpha+2cos\alpha}\\ =\dfrac{\dfrac{2sin\alpha}{cos\alpha}-\dfrac{3cos\alpha}{cos\alpha}}{\dfrac{3sin\alpha}{cos\alpha}+\dfrac{2cos\alpha}{cos\alpha}}\\ =\dfrac{2tan\alpha-3}{3tan\alpha+2}=\dfrac{2.3-3}{3.3+2}=\dfrac{3}{11}\)
Ta có: \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\quad (\alpha \ne {90^o})\)
\( \Rightarrow \frac{1}{{{{\cos }^2}\alpha }} = 1 + {3^2} = 10\)
\( \Leftrightarrow {\cos ^2}\alpha = \frac{1}{{10}} \Leftrightarrow \cos \alpha = \pm \frac{{\sqrt {10} }}{{10}}\)
Vì \({0^o} < \alpha < {180^o}\) nên \(\sin \alpha > 0\).
Mà \(\tan \alpha = 3 > 0 \Rightarrow \cos \alpha > 0 \Rightarrow \cos \alpha = \frac{{\sqrt {10} }}{{10}}\)
Lại có: \(\sin \alpha = \cos \alpha .\tan \alpha = \frac{{\sqrt {10} }}{{10}}.3 = \frac{{3\sqrt {10} }}{{10}}.\)
\( \Rightarrow P = \dfrac{{2.\frac{{3\sqrt {10} }}{{10}} - 3.\frac{{\sqrt {10} }}{{10}}}}{{3.\frac{{3\sqrt {10} }}{{10}} + 2.\frac{{\sqrt {10} }}{{10}}}} = \dfrac{{\frac{{\sqrt {10} }}{{10}}\left( {2.3 - 3} \right)}}{{\frac{{\sqrt {10} }}{{10}}\left( {3.3 + 2} \right)}} = \dfrac{3}{{11}}.\)
Cho sin = 1/3 với 90\(^o\)<\(\alpha\)<180\(^o\). Tính cos \(\alpha\) và tan (180\(^o\) - \(\alpha\))

\(90^0< a< 180^0\)
=>\(cosa< 0\)
\(sin^2a+cos^2a=1\)
=>\(cos^2a=1-\left(\dfrac{1}{3}\right)^2=\dfrac{8}{9}\)
mà cosa<0
nên \(cosa=-\dfrac{2\sqrt{2}}{3}\)
\(tan\left(180^0-a\right)=-tana=-\dfrac{sina}{cosa}\)
\(=-\dfrac{1}{3}:\dfrac{-2\sqrt{2}}{3}=\dfrac{1}{2\sqrt{2}}=\dfrac{\sqrt{2}}{4}\)

Bạn xem lại biểu thức A. Biểu thức $A$ sau khi rút gọn thì \(A=\frac{-2\sin ^2a}{3\cos 2a}\) vẫn phụ thuộc vào $a$
------------
Sử dụng công thức: \(\sin (90-a)=\cos a; \cot (90-a)=\tan a\), ta có:
\(B=\tan ^260(\sin ^8a-\cos ^8a)+4\cos 60(\cos ^6a-\sin ^6a)-\cos ^6a(\tan ^2a-1)^3\)
\(=3(\sin ^8a-\cos ^8a)+2(\cos ^6a-\sin ^6a)-\cos ^6a\left(\frac{\sin ^2a}{\cos ^2a}-1\right)^3\)
\(=3(\sin ^8a-\cos ^8a)+2(\cos ^6a-\sin ^6a)-(\sin ^2a-\cos ^2a)^3\)
\(=3(\sin ^2a-\cos ^2a)(\sin ^2a+\cos ^2a)(\sin ^4a+\cos ^4a)+2(\cos ^2a-\sin ^2a)(\cos ^4a+\sin ^2a\cos ^2a+\sin ^4a)-(\sin ^2a-\cos ^2a)^3\)
\(=3(\sin ^2-\cos ^2a)(\sin ^4a+\cos ^4a)-2(\sin ^2a-\cos ^2a)(\cos ^4a+\sin ^2a\cos ^2a+\sin ^4a)-(\sin ^2a-\cos ^2a)^3\)
\(=(\sin ^2a-\cos ^2a)[3(\sin ^4a+\cos ^4a)-2(\cos ^4a+\sin ^2a\cos ^2a+\sin ^4a)-(\sin ^2a-\cos ^2a)^2]\)
\(=(\sin ^2a-\cos ^2a).0=0\). Do đó giá trị của biểu thức không phụ thuộc vào $a$
a)
\(\begin{array}{l}\sin {168^o}45'33'' = 0,195;\\\cos {17^o}22'35'' = 0,954;\\\tan {156^o}26'39'' = - 0,436;\\\cot {56^o}36'42'' = 0,659\end{array}\)
b)
i) \(\alpha = {59^o}32'30,8''.\)
ii) \(\alpha = {124^o}32'28,65''.\)
iii) \(\alpha = {18^o}28'9,55''.\)