Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


* Dựng hình:
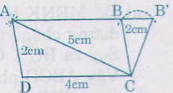
- Dựng tam giác ADC có AD = 2cm, DC = 4cm, CA = 5cm.
- Dựng tia Ax song song với CD.
- Đường tròn (C; 3cm) cắt Ax tại B1 và B2.
Hình thang ABCD với B ≡ B1 hoặc B ≡ B2 là hình thang cần dựng.
* Chứng minh
+ Tứ giác ABCD có AD = 2cm, DC = 4cm, CA = 5cm.
+ Ax // CD ⇒ AB // CD ⇒ ABCD là hình thang.
+ B ∈ (C; 3cm) ⇒ BC = 3cm.

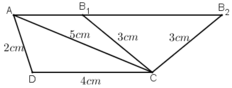
Dựng đoạn thẳng CD = 4cm.
- Dựng hai đường tròn (C, 5cm) và (D, 2cm) cắt nhau tại A.
- Dựng đường tròn (C, 2cm) và đường tròn (A, 4cm) cắt nhau tại B.
Đường thẳng AB kéo dài cắt đường tròn (C, 2cm) tại điểm B' (ngoài điểm B đã kể ở trên)
Các tứ giác ABCD và AB'CD là những hình thang thỏa mãn đề bài.
Chứng minh: Vì B thuộc đường tròn (A, 4cm) nên AB = 4cm.
ΔABC = ΔDCA (AB = CD = 4cm, AD = BC = 2cm, AC chung) do đó góc BAC = góc DCA là cặp so le trong ta có: AB // CD.
Tứ giác ABCD có AB // CD, AD = 2cm, CD = 4cm, BC = 2cm là hình thang thỏa mãn yêu cầu, AB'CD cũng là hình thang thỏa mãn yêu cầu vì AB' // CD, AD = 2cm, CD = 4cm, CB' = 2cm.

Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn bài toán.
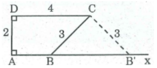
Ta thấy ∆ ADC xác định được vì biết AD = 2cm, ∠ D = 90 0 , DC = 4cm. Ta cần xác định đỉnh B. Đỉnh B thỏa mãn hai điều kiện:
- B nằm trên tia Ax//CD
- B cách C một khoảng bằng 3cm
Cách dựng:
- Dựng ΔADC biết:
AD = 2cm, ∠ D = 90 0 , DC = 4cm
- Dựng Ax ⊥ AD
- Dựng cung tròn tâm C bán kính bằng 3cm, cắt Ax tại B.
Nối BC ta có hình thang ABCD dựng được.
Chứng minh:
Thật vậy theo cách dựng, ta có: AB // CD , ∠ D = 90 0
Tứ giác ABCD là hình thang vuông
Lại có AD = 2cm, CD = 4cm, BC = 3cm
Hình thang dựng được thỏa mãn điều kiện bài toán.
Biện luận: ∆ ADC dựng được, hình thang ABCD luôn dựng được.
Bài toán có hai nghiệm hình.

Kẻ BH//AD(H∈CD)BH//AD(H∈CD), kẻ BD
Ta có:
+) AB//CD (hình thang ABCD)
⇒B2ˆ=D1ˆ⇒B2^=D1^ ( 2 góc so le trong )
+) BH//AD (cách vẽ)
⇒D2ˆ=B1ˆ⇒D2^=B1^ ( 2 góc so le trong)
Xét ΔDABΔDAB và ΔBHDΔBHD, ta có:
B2ˆ=D1ˆ(cmt)B2^=D1^(cmt)
BD : chung
D2ˆ=B1ˆ(cmt)D2^=B1^(cmt)
⇒⇒ ΔDABΔDAB = ΔBHDΔBHD (gcg)
⇒AD=BH⇒AD=BH
mà AD=3cm(gt)AD=3cm(gt)
⇒BH=3cm⇒BH=3cm
+) ΔDABΔDAB = ΔBHDΔBHD (cmt)
⇒AB=DH⇒AB=DH
mà AB=4cm(gt)AB=4cm(gt)
⇒DH=4cm⇒DH=4cm
+) DH+HC=DC(H∈DC)DH+HC=DC(H∈DC)
⇒4+HC=8⇒4+HC=8
⇒HC=4cm⇒HC=4cm
Xét ΔBHC,ΔBHC, ta có:
52=32+4252=32+42
⇒BC2=BH2+HC2⇒BC2=BH2+HC2 (Định lý Py-ta-go)
⇒ΔBHC⇒ΔBHC vuông tại H
⇒H1ˆ=900⇒H1^=900
+) AD//BH
⇒ADHˆ=H1ˆ⇒ADH^=H1^ (2 góc động vị)
⇒ADHˆ=900⇒ADH^=900
⇒⇒ Hình thang ABCD là hình thang vuông