Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta biết tập nghiệm của phương trình ax + by = c được biểu diễn bằng đường thẳng ax + by = c và tập nghiệm của phương trình a'x + b'y = c' được biểu diễn bằng đường thẳng a'x + b'y = c'.
Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
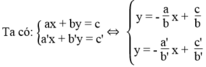
Hệ phương trình vô nghiệm khi hai đường thẳng song song nhau. Nghĩa là hai đường thẳng có hệ số góc bằng nhau và tung độ gốc khác nhau:
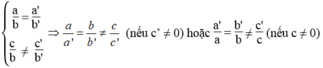
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn vô nghiệm:
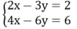
Vì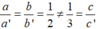 
nên hệ phương trình trên vô nghiệm
Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
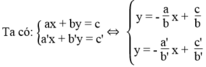
Hệ phương trình có một nghiệm duy nhất khi hai đường thẳng cắt nhau. Nghĩa là hai đường thẳng có hệ số góc khác nhau:
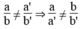
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn vô nghiệm:
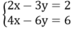
Vì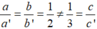 
nên hệ phương trình trên vô nghiệm
Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
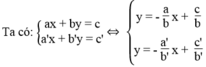
Hệ phương trình có vô số nghiệm khi hai đường thẳng trùng nhau. Nghĩa là hai đường thẳng có hệ số góc và tung độ gốc bằng nhau:
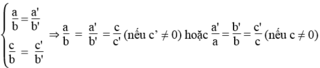
*a = 0, a’ ≠ 0
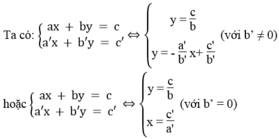
Vì hai đường thẳng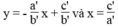 
luôn luôn cắt trục hoành còn đường thẳng y = c/b song song hoặc trùng với trục hoành nên chúng luôn luôn cắt nhau.
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
*a = a’ = 0
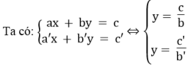
Hệ có vô số nghiệm khi hai đường thẳng trùng nhau, nghĩa là:
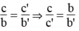
Hệ vô nghiệm khi hai đường thẳng song song nhau, nghĩa là:
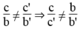
*b = 0, b’ ≠ 0
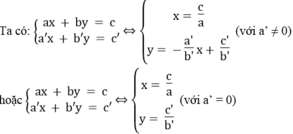
Vì hai đường thẳng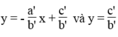 
luôn luôn cắt trục tung còn đường thẳng x = c/a song song hoặc trùng với trục tung nên chúng luôn luôn cắt nhau.
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
*b = b’ = 0
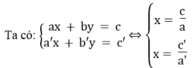
Hệ có vô số nghiệm khi hai đường thẳng trùng nhau, nghĩa là:
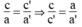
Hệ vô nghiệm khi hai đường thẳng song song nhau, nghĩa là:
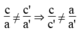
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn có vô số nghiệm:
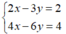
Vì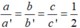 
nên hệ phương trình có vô số nghiệm
Bài 1 : Giải
Đồ thị đi qua A ( -1 ; -3 ) và B ( 0 ; 2 )
Ta có hệ phương trình :
\(\hept{-a+b=-3b=2\Leftrightarrow\hept{\begin{cases}a=5\\b=2\end{cases}}}\)
=> y = 5x + 2
b) \(\hept{\begin{cases}-x+y=1\left(d_1\right)\\2x-2y=2\left(d_2\right)\end{cases}}\)
Ta có : \(\frac{-1}{2}=\frac{1}{-2}\ne\frac{1}{2}\)
=> d1 // d2
=> hệ ( I ) vô nghiệm
Bài 2 : Giải
Gọi thời gian mộit vòi chảy một mình đến khi đầy bể lần lượt là x , y giờ
Mỗi giờ vòi 1 chảy được \(\frac{1}{x}\)bể ,vòi 2 chảy được \(\frac{1}{y}\)bể
5 giờ 50 phút = \(\frac{35}{6}\)giờ
=> Mỗi giờ cả 2 vòi cũng chảy được \(1:\frac{35}{6}=\frac{6}{35}\)bể
=> \(\frac{1}{x}+\frac{1}{y}=\frac{6}{35}\) ( 1 )
Cả 2 vòi chảy 5 giờ thì được : \(5.\frac{6}{35}=\frac{6}{7}\) bể
Vòi 2 chảy một mình thêm 2 giờ được \(2.\frac{1}{y}\)bể
=> \(\frac{6}{7}+2.\frac{1}{y}=1\Rightarrow\frac{1}{y}=\frac{1}{14}\Rightarrow\frac{1}{x}=\frac{1}{10}\)
=> x = 10 ; y = 14
Vậy để chảy một mình đến khi đầy bể , vòi 1 chảy trong 10 giờ ,vòi 2 chảy trong 14 giờ
6:
a: f(-2)=-1/2*(-2)^2=-2
=>Loại
b: f(4)=-1/2*4^2=-8=yB
=>B thuộc (P)
c: f(2)=-1/2*2^2=-2
=>Loại
5: f(-2)=-1/4*(-2)^2=-1/4*4=-1
=>A thuộc (P)
4: tính chất:
Nếu a>0 thì hàm số đồng biến khi x>0 và nghịch biến khi x<0
Nếu a<0 thì hàm số đồng biến khi x<0 và nghịch biến khi x>0
y=1/2x^2: Hàm số đồng biến khi x>0 và nghịch biến khi x<0
y=-3x^2: Hàm số đồng biến khi x<0 và nghịch biến khi x>0
\(\hept{\begin{cases}mx+2my=m+1\\x+\left(m+1\right)y=2\end{cases}\Leftrightarrow\hept{\begin{cases}x+2y=\frac{m+1}{m}\\x+\left(m+1\right)y=2\end{cases}\Leftrightarrow}\hept{\begin{cases}\left(m-1\right)y=2-\frac{m+1}{m}\\x+2y=\frac{m+1}{m}\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(m-1\right)y=\frac{m-1}{m}\\x+2y=\frac{m+1}{m}\end{cases}}}\)
bình thường dùng pp thế nhưng chắc bài này cộng là nhanh nhất rồi ( ͡° ͜ʖ ͡°)
với m=1 thì y vô số nghiệm => x vô số nghiệm thỏa mãn pt dưới
Với \(m\ne1\Rightarrow y=\frac{1}{m}\Rightarrow x=\frac{m+1}{m}-\frac{2}{m}=\frac{m-1}{m}\)
b/ \(A\left(\frac{m-1}{m};\frac{1}{m}\right)\)
I/Vì x=1-y nên A luôn nằm trên đồ thị hàm số x=1-y
II/ Để A thuộc góc phân tư thứ nhất thì x>0, y>0, \(\Leftrightarrow\hept{\begin{cases}1-\frac{1}{m}>0\\\frac{1}{m}>0\end{cases}\Leftrightarrow\hept{\begin{cases}\frac{1}{m}< 1\\m>0\end{cases}\Leftrightarrow}m>1}\)
Vậy với m>1 thì A thuộc góc phần tư thứ nhất
III/ Cái này thì bạn tự vẽ hình, kẻ đường cao xuống rồi dùng hệ thức lượng liên hệ giữa đường cao và cạnh góc vuông tính
Đặt S=x+y, P=x.y
Ta có:S=2a-1, x^2+y^2=S^2-2P=a^2+2a-3
\Rightarrow P=\frac{1}{2}[(2a-1)^2-(a^2+2a-3)]=\frac{1}{2}(3a^2-6a+4)
Trước hết tìm a để hệ có nghiệm.
Điều kiện để hệ có nghiệm:S^2-4P \geq 0 \Leftrightarrow (2a-1)^2-2(3a^2-6a+4)\geq 0
\Leftrightarrow -2a^2+8a-7 \geq 0 \leftrightarrow 2-\frac{\sqrt{2}}{2} \leq a \leq 2+\frac{\sqrt{2}}{2} (1)
Tìm a để P=\frac{1}{2}(3a^2-6a+4) đạt giá trị nhỏ nhất trên đoạn
[2-\frac{\sqrt{2}}{2} ;2+\frac{\sqrt{2}}{2}]
Ta có hoành độ đỉnh a_0=\frac{6}{2.3}=1Parabol có bề lõm quay lên do đó \min P=P(2-\frac{\sqrt{2}}{2} )$
Vậy với a=2-\frac{\sqrt{2}}{2} thì xy đạt giá trị nhỏ nhất.
Ta biết tập nghiệm của phương trình ax + by = c được biểu diễn bằng đường thẳng ax + by = c và tập nghiệm của phương trình a'x + b'y = c' được biểu diễn bằng đường thẳng a'x + b'y = c'.