Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án:
Gọi $n_{Na_2CO_3};n_{H_2O}$ lần lượt a;b(mol)
Bảo toàn O ta có: \(4a+0,925.2=3a+b+1,075.2\Rightarrow a-b=0,3\)
Bảo toàn khối lượng ta có: \(117,6+0,925.32=106a+18b+1,075.44\Rightarrow138a+18b=99,9\)
Giải hệ ta được \(\left\{{}\begin{matrix}a=0,675\\b=0,375\end{matrix}\right.\)
Gọi CTTQ của ancol là $C_nH_{2n+2}O$
Suy ra $n_{ancol}=1,35(mol)$
Do đó $n=\frac{38}{27}$
Quy hỗn hợp về \(\left\{{}\begin{matrix}HCOOCH_3:x\left(mol\right)\\CH_2=CH-COOCH_3:y\left(mol\right)\\\left(COOCH_3\right)_2:z\left(mol\right)\\CH_2:t\left(mol\right)\end{matrix}\right.\)
Ta có: \(x+y+z=0,85\)
Bảo toàn nguyên tố K ta có: $n_{KOH}=1,35(mol)$
Bảo toàn khối lượng ta có: \(m_{hh}=50,9+117,6-1,35.56=92,9\left(g\right)\)
Suy ra \(60x+86y+118z+14t=92,9\)
Bảo toàn mol K trong muối ta có: \(x+y+2z=1,35\)
Bảo toàn C ta có: \(2x+4y+4z+t=1,075+0,675+\frac{38}{27}.1,35=3,65\)
Giải hệ ta được \(\left\{{}\begin{matrix}x=0,15\\y=0,2\\z=0,5\\t=0,55\end{matrix}\right.\)
Gộp nhóm ta thu được các chất là \(\left\{{}\begin{matrix}HCOOC_2H_5:0,15\left(mol\right)\\CH_2=CH-COOC_3H_7:0,2\left(mol\right)\\\left(COOCH_3\right)_2:0,5\left(mol\right)\end{matrix}\right.\)
Từ đó suy ra %m
Khi cho A td KOH thu được ancol đồng đẳng. => Các ancol là no đơn chức mạch hở.
Gọi CT các este: \(C_mH_{2m+1}COOC_{m'}H_{2m'+1};C_nH_{2n-1}COOC_{n'}H_{2n'+1};C_qH_{2q}\left(COOC_{q'}H_{2q'+1}\right)_2\)
TN2: Đốt hỗn hợp 3 muối.
Đặt \(n_{K_2CO_3}=x;n_{H_2O}=y\left(mol\right)\)
\(BTNT.K\Rightarrow n_{COOK^-}=2n_{K_2CO_3}=2x\left(mol\right)\\ BTNT.O\Rightarrow2n_{COOK^-}+2n_{O_2}=3n_{K_2CO_3}+2n_{CO_2}+n_{H_2O}\\ \Rightarrow x-y=0,3\\ BTKL\Rightarrow m_{M'}+m_{O_2}=m_{K_2CO_3}+m_{CO_2}+m_{H_2O}\\ \Rightarrow138x+18y=99,9\\ \Rightarrow\left\{{}\begin{matrix}x=0,675\\y=0,375\end{matrix}\right.\)
H2 muối gồm: \(C_mH_{2m+1}COOK\text{ }a\text{ }mol;C_nH_{2n-1}COOK\text{ }b\text{ }mol;C_qH_{2q}\left(COOK\right)_2\text{ }c\text{ }mol\)
\(\Rightarrow n_A=a+b+c=0,85\\ BTNT.C\Rightarrow\left(m+1\right)a+\left(n+1\right)b+\left(q+2\right)c=n_{K_2CO_3}+n_{CO_2}=1,75\\ \Rightarrow ma+nb+qc=0,4\\ BTNT.K\Rightarrow a+b+2c=1,35\\ BTNT.H\Rightarrow\left(2m+1\right)a+\left(2n-1\right)b+2qc=2n_{H_2O}=0,75\\ \Rightarrow a-b=-0,05\\ \Rightarrow\left\{{}\begin{matrix}a=0,15\\b=0,2\\c=0,5\end{matrix}\right.\\ \Rightarrow0,15m+0,2n+0,5q=0,4\)
Do \(m;q\ge0\Rightarrow n\le\frac{0,4}{0,2}=2\)
Mà \(n\ge2\Rightarrow n=2\Rightarrow m=q=0\)
TN1: Do các ancol đơn chức => \(n_{ancol}=n_{KOH}=2n_{K_2CO_3}=1,35\)
\(\Rightarrow\overline{M_{ancol}}=\frac{50,9}{1,35}=37,7\) => Có 1 ancol là \(CH_3OH\)
Nếu CH3OH là Cm'H2m'+1OH \(\Rightarrow n_{CH_3OH}=n_{HCOOK}=0,15\left(mol\right)\)
\(\Rightarrow m_{ancol}=0,15\cdot32+0,2\left(14n'+18\right)+\left(14q'+18\right)=50,9\\ \Rightarrow n'+5q'=8,75\left(L\right)\)
Nếu CH3OH là Cn'H2n'+1OH \(\Rightarrow n_{CH_3OH}=n_{C_2H_3COOK}=0,2\left(mol\right)\)
\(\Rightarrow m_{ancol}=0,15\left(14m'+18\right)+0,2\cdot32+\left(14q'+18\right)=50,9\\ \Rightarrow3n'+20q'=34\\ \Rightarrow q'=\frac{34-3n'}{20}\le\frac{34-3\cdot2}{20}=1,4\left(L\right)\)
Nếu CH3OH là Cq'H2q'+1OH \(\Rightarrow n_{CH_3OH}=2n_{\left(COOK\right)_2}=1\left(mol\right)\)
\(\Rightarrow m_{ancol}=0,15\left(14m'+18\right)+0,2\left(14n'+18\right)+0,5\cdot32=50,9\\ \Rightarrow3m'+4n'=18\\ \Rightarrow n'=\frac{18-3m'}{4}\le\frac{18-3\cdot2}{4}=3\\ \Rightarrow n'=3;m'=2\)
Các este là: \(HCOOC_2H_5;C_2H_3COOC_3H_7;COOCH_3-COOCH_3\)
CTCT:
\(HCOO-CH_2-CH_3\\ CH_2=CH-COO-CH_2-CH_2-CH_3\\ COOCH_3-COOCH_3\)
% KL: \(11,95\%HCOOC_2H_5;24,54\%C_2H_3COOC_3H_7;63,51\%COOCH_3-COOCH_3\)

a) Bảo toàn khối lượng:
\(a,m_{H_2}=m_{hhM}-m_{hhZ}=1,5\left(g\right)\\ \Rightarrow n_{H_2}=\dfrac{1,5}{2}=0,75\left(mol\right)\\ \Rightarrow n_M=0,75\left(mol\right)\\ n_{CO_2}=\dfrac{52,8}{44}=1,2\left(mol\right)\\ \Rightarrow\overline{C}=\dfrac{n_{CO_2}}{n_M}=\dfrac{1,2}{0,75}=1,6\)
Sơ đồ đường chéo, ta được 2 anđehit cần tìm:
\(\left\{{}\begin{matrix}HCHO:0,3\left(mol\right)\\CH_3CHO:0,45\left(mol\right)\end{matrix}\right.\\ \Rightarrow\%m_{HCHO}=\dfrac{0,3.30}{0,3.30+0,45.44}.100=31,25\%\\ \Rightarrow\%m_{CH_3CHO}=68,75\%\)
b) hh Z tráng gương sẽ tạo số mol Ag là:
\(n_{Ag}=4.n_{HCHO}+2.n_{CH_3CHO}=4.0,3+2.0,45=2,1\left(mol\right)\\ \Rightarrow m_{\downarrow}=m_{Ag}=2,1.108=226,8\left(g\right)\)

nCO2 = 2,688/22,4 = 0,12 mol; nH2O = 2,52/18 = 0,14 mol
Ta thấy nH2O>nCO2 => ancol là ancol no, đơn chức, mạch hở
Gọi công thức chung của ancol là CkH2k+2O (k €N*)
Giả sử:
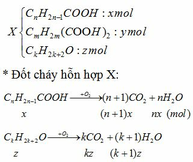
=> nH2O – nCO2 = nx – (n+1)x + (m+1)y – (m+2)y + (k+1)z – kz
=> 0,14 – 0,12 = -x - y + z hay -x - y + z = 0,02 (1)
BTNT ta tính được số mol của các nguyên tố:
nC = nCO2 = 0,12 mol
nH = 2nH2O = 2.0,14 = 0,28 mol
nO = 2nCnH2n-1COOH + 4nCmH2m(COOH)2 + nCkH2k+2O = 2x + 4y + z
=> mX = mC + mH + mO = 0,12.12 + 0,28.1 + 16(2x + 4y + z) = 32x + 64y + 16z + 1,72
* Phản ứng este hóa: Do sau phản ứng chỉ thu được chất có chứa chức este nên axit và ancol phản ứng vừa đủ
n ancol = x + 2y = z hay x + 2y – z = 0 (2)
BTKL ta có: mX = m este + mH2O => 32x + 64y + 16z + 1,72 = 3,22 + 18(x+2y)
hay 14x + 28y + 16z = 1,5 (3)
Từ (1) (2) (3) ta có hệ phương trình:
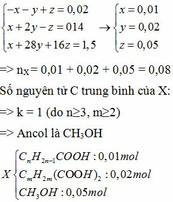
Bảo toàn nguyên tố C ta có: 0,01n + 0,02m + 0,05.1 = 0,12
=> n +2m = 7 mà do n≥3, m≥2 nên chỉ có cặp n = 3, m = 2 thỏa mãn
Vậy các axit trong X là: CH2=CH-COOH và HOOC-COOH.
Kết luận: Hỗn hợp X gồm các chất CH2=CH-COOH, HOOC-COOH và CH3OH.
- Một số ứng dụng của PVC trong thực tế như làm ống dẫn nước, vỏ dây điện, đồ giả da, áo mưa, nhãn chai nước khoáng, …

Ta có:
\(\left\{{}\begin{matrix}n_{CO2}=0,4\left(mol\right)\\n_{H2O}=0,56\left(mol\right)\end{matrix}\right.\Rightarrow n_{ancol}=n_{H2O}-n_{CO2}=0,56-0,4=0,16\left(mol\right)\)
\(\Rightarrow C=\frac{0,4}{0,56-0,4}=2,5\)
Vậy CT của 2 ancol là C2H5OH và C3H7OH
Gọi \(\left\{{}\begin{matrix}n_{C2H5OH}:x\left(mol\right)\\n_{C3H7OH}:y\left(mol\right)\end{matrix}\right.\)
Giải hệ PT:
\(\left\{{}\begin{matrix}2x+3y=0,4\\x+y=0,16\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=0,08\\y=0,08\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{C2H5OH}=\frac{0,08.46}{0,08.\left(46+60\right)}.100\%=43,40\%\\\%m_{C3H7OH}=100\%-43,40\%=56,60\%\end{matrix}\right.\)