
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


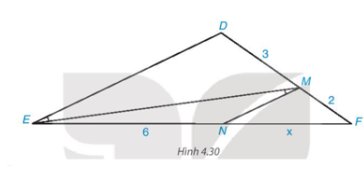
Trong Hình 4.30 có \(\widehat {DEM} = \widehat {EMN}\) mà hai góc này ở vị trí so le trong nên MN // DE.
Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:
\(\dfrac{{MF}}{{M{\rm{D}}}} = \dfrac{{NF}}{{NE}}\) hay \(\dfrac{2}{3} = \dfrac{x}{6}\)
Suy ra \(x = \dfrac{{2.6}}{3} = 4\) (đvđd).
Vậy x = 4 (đvđd).

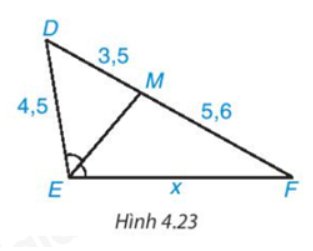
Trong Hình 4.23 có \(\widehat {DME} = \widehat {MEF}\) nên EM là tia phân giác của \(\widehat {{\rm{DEF}}}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{E{\rm{D}}}}{{EF}} = \dfrac{{M{\rm{D}}}}{{MF}}\) hay \(\dfrac{{4,5}}{x} = \dfrac{{3,5}}{{5,6}}\)
Suy ra: \(x = \dfrac{{5,6.4,5}}{{3,5}} = 7,2\)(đvđd)
Vậy x = 7,2 (đvđd).

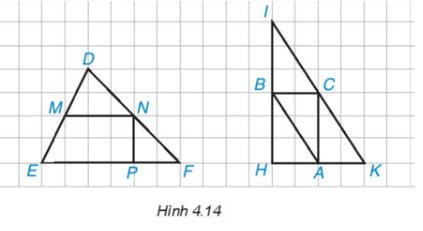
Đường trung bình trong tam giác DEF là: cạnh MN.
Đường trung bình trong tam giác HIK là: cạnh BC, CA, AB.
Quan sát Hình 4.14, ta thấy:
* Xét ∆DEF có M là trung điểm của cạnh DE; N là trung điểm của cạnh DF nên MN là đường trung bình của ∆DEF.
* Xét ∆IHK có:
• B là trung điểm của cạnh IH; C là trung điểm của cạnh IK nên BC là đường trung bình của ∆DEF.
• B là trung điểm của cạnh IH; A là trung điểm của cạnh HK nên AB là đường trung bình của ∆DEF.
• A là trung điểm của cạnh HK; C là trung điểm của cạnh IK nên AC là đường trung bình của ∆DEF.
Vậy đường trung bình của ∆DEF là MN; các đường trung bình của ∆IHK là AB, BC, AC.

• Hình 3.51a)
Tứ giác đã cho có hai đường chéo cắt nhau tại trung điểm của mỗi đường và chúng vuông góc với nhau nên tứ giác đó là hình thoi.
• Gọi tứ giác trong Hình 3.51b) là tứ giác ABCD.
Vì \(\widehat {{B_1}} = \widehat {{D_1}}\) mà hai góc này ở vị trí so le trong nên AB // CD.
Mà AB = CD nên tứ giác ABCD là hình bình hành.
Mặt khác, \(\widehat {{D_1}} = \widehat {{D_2}}\) hay DB là tia phân giác của \(\widehat {A{\rm{D}}C}\)
Khi đó, hình bình hành ABCD có DB là tia phân giác của \(\widehat {A{\rm{D}}C}\).
Do đó tứ giác ABCD là hình thoi.
• Tứ giác trong Hình 3.51c) hai đường chéo vuông góc với nhau và có đường chéo là đường vuông góc của một góc của tứ giác.
Từ đó ta suy ra tứ giác đã cho không phải là hình thoi.
Vậy Hình 3.51a và Hình 3.51b là hình thoi.

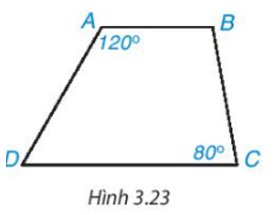
Để hình thang ABCD là hình thang cân thì \(\widehat A = \widehat B = {120^o};\widehat C = \widehat D = {80^o}\)
Suy ra \(\widehat A + \widehat B + \widehat C + \widehat D\)=120°+120°+80°+80°=400°>360°(không thỏa mãn định lí tổng bốn góc trong một tứ giác).
Khi đó, ABCD không phải là tứ giác.
Do đó ABCD cũng không phải là hình thang cân.

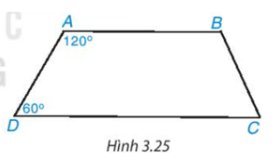
Do \(\widehat{A}+\widehat{D}=120^o+60^o=180^o\)
\(\Rightarrow AB//CD\)
\(\Rightarrow\) ABCD là hình thang.

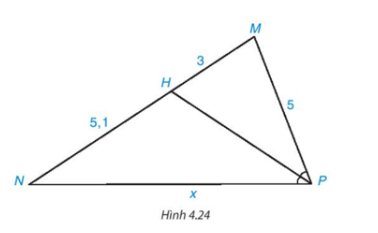
Trong Hình 4.24 có \(\widehat {MPH} = \widehat {NPH}\) nên PH là tia phân giác của \(\widehat {MPN}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{MP}}{{NP}} = \dfrac{{MH}}{{NH}}\) hay \(\dfrac{5}{x} = \dfrac{3}{{5,1}}\)
Suy ra \(x = \dfrac{{5.5,1}}{3} = 8,5\) (đvđd).
Vậy x = 8,5 (đvđd).

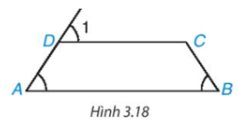
Ta có \(\widehat A = \widehat {{D_1}}\) mà hai góc này ở vị trí đồng vị nên AB // CD.
Suy ra tứ giác ABCD là hình thang.
Mặt khác hình thang ABCD có \(\widehat A = \widehat B\) nên ABCD là hình thang cân.
Do đó AD = BC (đpcm).

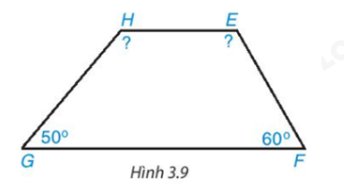
Áp dụng định lí tổng bốn góc trong một tứ giác vào tứ giác HEFG, ta có:
\(\widehat H + \widehat E + \widehat F + \widehat G = {360^o}\)
\(\widehat E\)+10°+\(\widehat E\)+60°+50°=360o
2\(\widehat E\)+120°=360°
Suy ra 2\(\widehat E\)=360°−120°=240°
Khi đó \(\widehat E\)=120°
Suy ra \(\widehat H\)=\(\widehat E\)+10°=120°+10°=130°
Vậy \(\widehat H\)=130°; \(\widehat E\)= 120°


Đáp án đúng là: C
Trong Hình 4.31 có \(\widehat {AMN} = \widehat {ABC}\) mà hai góc này ở vị trí đồng vị nên MN // BC.
Áp dụng định lí Thalès vào tam giác ABC, ta có:
\(\dfrac{{AM}}{{BM}} = \dfrac{{AN}}{{CN}}\) hay \(\dfrac{2}{3} = \dfrac{{1,5}}{x}\)
Suy ra \(x = \dfrac{{1,5.3}}{2} = 2,25\)
Vậy x = 2,25.