K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
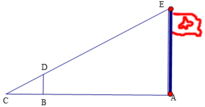
Cùng một thời điểm thì góc tạo bởi tia nắng và mặt đất là như nhau. Do đó, \(\widehat {EFD} = \widehat {BCA}\).
Xét tam giác \(DEF\) và tam giác \(ABC\) ta có:
\(\widehat {EFD} = \widehat {BCA}\) (chứng minh trên)
\(\widehat {EDF} = \widehat {BAC} = 90^\circ \).
Do đó, \(\Delta DEF\backsim\Delta ABC\) (g.g)
Suy ra, \(\frac{{FD}}{{AC}} = \frac{{ED}}{{AB}} \Leftrightarrow \frac{{1,8}}{6} = \frac{{2,4}}{{AB}} \Rightarrow AB = \frac{{6.2,4}}{{1,8}} = 8\).
Vậy cột cờ \(AB\) cao 8m.

HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
Bác Dương đã chứng minh ΔAEB ∽ ΔDEC và tìm tỉ số đồng dạng của chúng từ đó tính được chiều cao của cột đèn
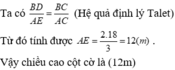
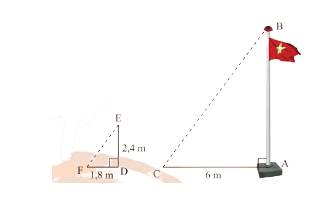

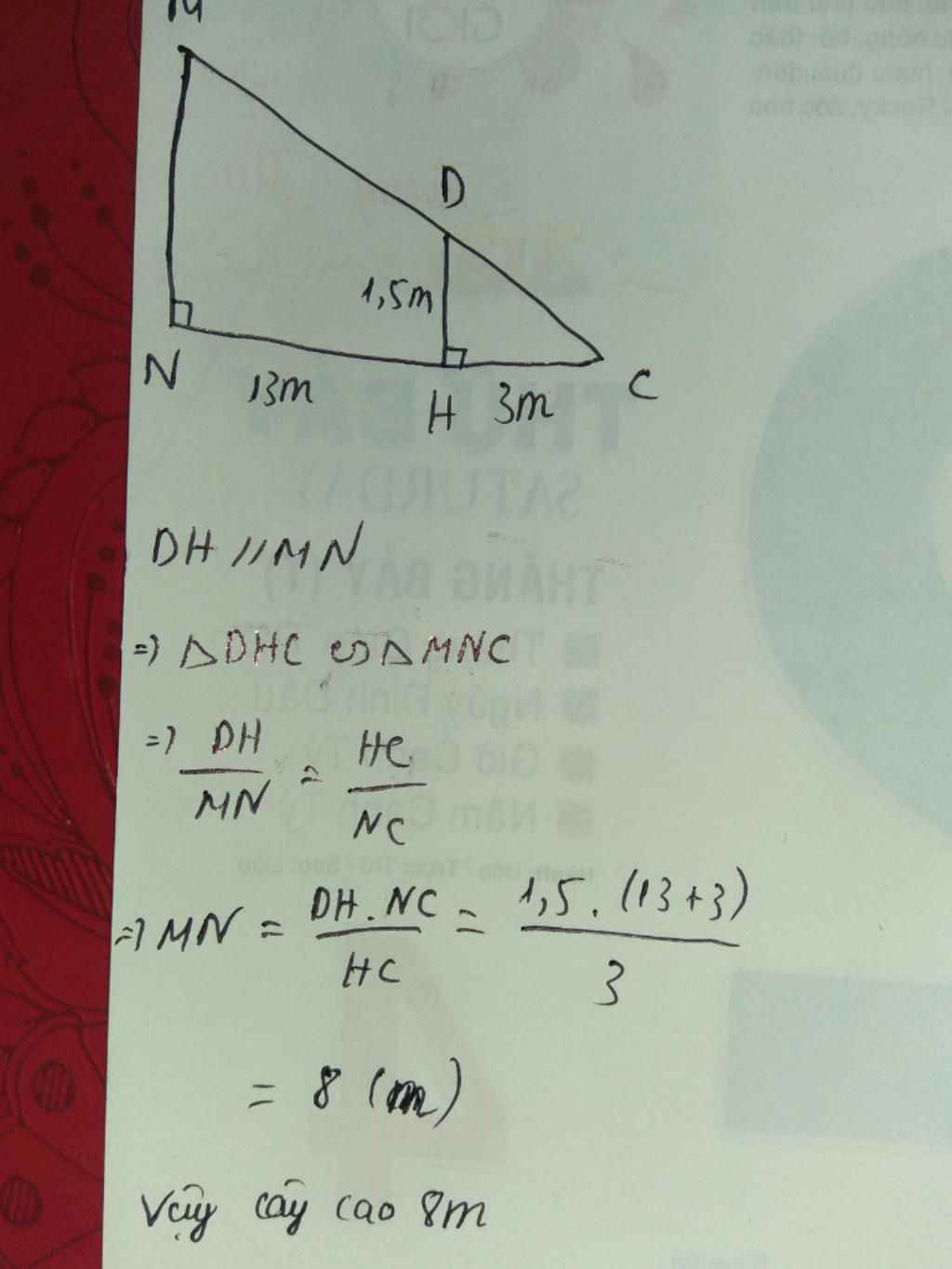
xét ΔACE và ΔABD
\(\widehat{ABD}=\widehat{ACE}=90^o\left(gt\right)\)
\(\widehat{A}\) chung
->ΔACE ∼ ΔABD
->\(\dfrac{AB}{AC}=\dfrac{BD}{CE}\) hay \(\dfrac{2}{2+4}=\dfrac{1,5}{CE}\)
=>\(CE=\dfrac{\left(2+4\right).1,5}{2}=4,5\left(m\right)\)