Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nước ngọt loại 1: pha được tối đa 6 lít nếu chỉ pha loại này ; nước ngọt loại 2: pha được tối đa 7 lít nếu chỉ pha loại này (dựa trên lượng sử dụng tối đa của hương liệu)
Vì 1 lít nước ngọt loại 1 được tính điểm cao hơn loại 2 \(\Rightarrow\)Chọn pha nước ngọt loại 1 trước
6 lít là max của nước ngọt loại 1 \(\Rightarrow\) Pha 5 lít nước ngọt loại 1 \(\Rightarrow\)Tốn 50 gam đường, 5 lít nước, 20 gam hương liệu
Còn được pha 160 gam đường, 4 lít nước, 4 gam hương liệu \(\Rightarrow\)Pha 4 lít nước ngọt loại 2.
\(\Rightarrow\)Số điểm thưởng cao nhất: 5 lít loại 1 = 5.80 =400 ; 4 lít loại 2 = 4.60 = 240 ; 400 + 240 = 640 (điềm)

Tham khảo:
a) Gọi x là số lít nước cam loại A, y là là số lít nước cam loại B nên pha. Ta có hệ bất phương trình:
\(\left\{ \begin{array}{l}30x + 10y \le 210\\x + 4y \le 24\\x + y \le 9\\x \ge 0\\y \ge 0\end{array} \right.\)
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy, ta được như hình dưới.
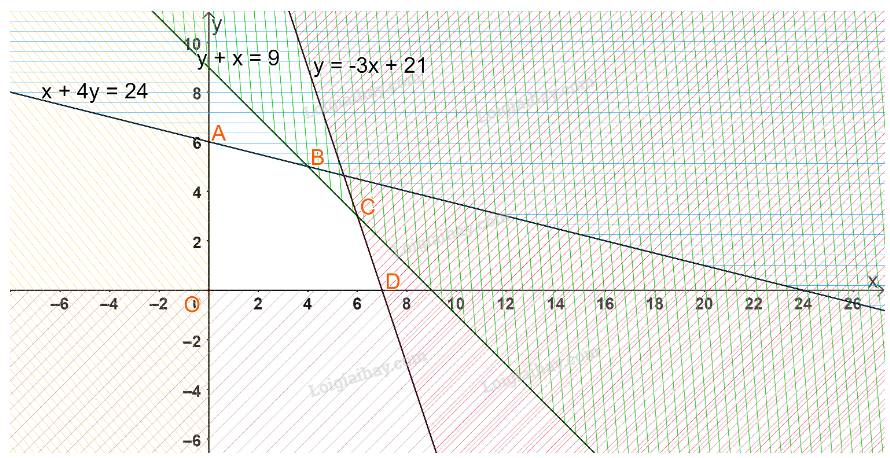
Miền nghiệm là miền không gạch chéo (miền ngũ giác OABCD) với các đỉnh O (0;0), A (0;6), B (4;5), C(6;3), D(7;0)
Doanh thu F=60x+80y (nghìn đồng)
Ta có:
Tại O(0;0): F(0;0)=60.0+80.0=0
Tại A(0;6): F(0;6)=60.0+80.6=480
Tại B(4;5): F(4;5)=60.4+80.5=640
Tại C(6;3): F(6;3)=60.6+80.3=600
Tại D(7;0): F(7;0)=60.7+80.0=420
=> GTLN của F bằng 640 (nghìn đồng) tại x=4 và y=5.
Vậy người đó nên pha chế 4l nước cam loại A và 5l nước cam loại B để có doanh thu cao nhất.

mn giúp em với câu này thi thpt quốc gia 2015 nhưng là thưởng 60đ cho 1lit nước cam , em tính ko ra trong 2 đáp án trên

Gọi phương trình đường thẳng \(d:ax + by + c = 0\)
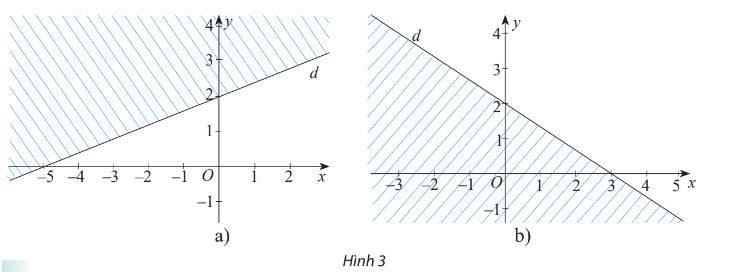
a) Từ hình a) ta thấy d đi qua hai điểm\(A(0;2)\) và \(B( - 5;0)\)
\( \Rightarrow \left\{ \begin{array}{l}b.2 + c = 0\\ - 5a + c = 0\end{array} \right. \Rightarrow c = 5a = - 2b\)
Chọn \(a = 2 \Rightarrow b = - 5;c = 10\) và \(d:2x - 5y + 10 = 0\)
Điểm O (0;0) thuộc miền nghiệm và \(2.0 - 5.0 + 10 = 10 > 0\)
Vậy bất phương trình cần tìm là \(2x - 5y + 10 > 0\)
b) Từ hình b) ta thấy d đi qua hai điểm\(A(0;2)\) và \(B(3;0)\)
\( \Rightarrow \left\{ \begin{array}{l}2b + c = 0\\3a + c = 0\end{array} \right. \Rightarrow - c = 3a = 2b\)
Chọn \(a = 2 \Rightarrow b = 3;c = - 6\) và \(d:2x + 3y - 6 = 0\)
Điểm O (0;0) không thuộc miền nghiệm và \(2.0 + 3.0 - 6 = - 6 < 0\)
Vậy bất phương trình cần tìm là \(2x + 3y - 6 > 0\)

Tham khảo:
Để pha x lít nước cam loại I cần 30x g bột cam,
Để pha y lít nước cam loại II cần 20y g bột cam,
Vì Cúc chỉ có thể dùng không quá 100 gam bột cam nên ta có bất phương trình \(30x + 20y \le 100\)
\( \Leftrightarrow 3x + 2y - 10 \le 0\)
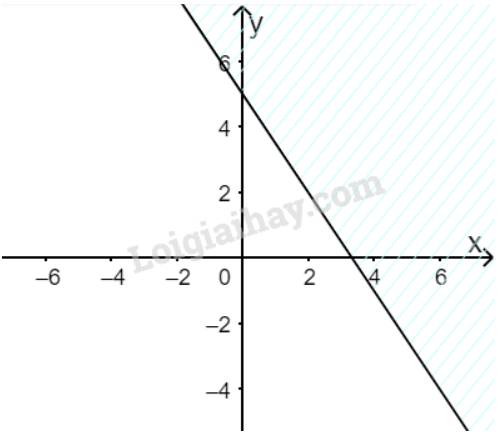
Vẽ đường thẳng \(\Delta :3x + 2y - 10 = 0\) đi qua hai điểm \(A(0;5)\) và \(B\left( {2;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(3.0 + 2.0 - 10 = - 10 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)

Sửa đề: giảm đi 100 lượt
Gọi số tiền cần tăng thêm của 1 cốc là x(nghìn đồng)
=>Giá 1 ly sau khi tăng là x+20
=>Số lượt khách sau khi tăng là 4000-100x
=>Tổng doanh thu là S=(20+x)(4000-100x)
S'=4000-100x+(20+x)(-100)=2000-200x=0
=>x=10
=>S đạt maxkhi x=10
=>giá 1 cốc trà sữa cần bán là 20+10=30(ngàn đồng)

mk nghĩ các bạn bt cũng giải được bạn ko cần nói các bạn thông minh đâu