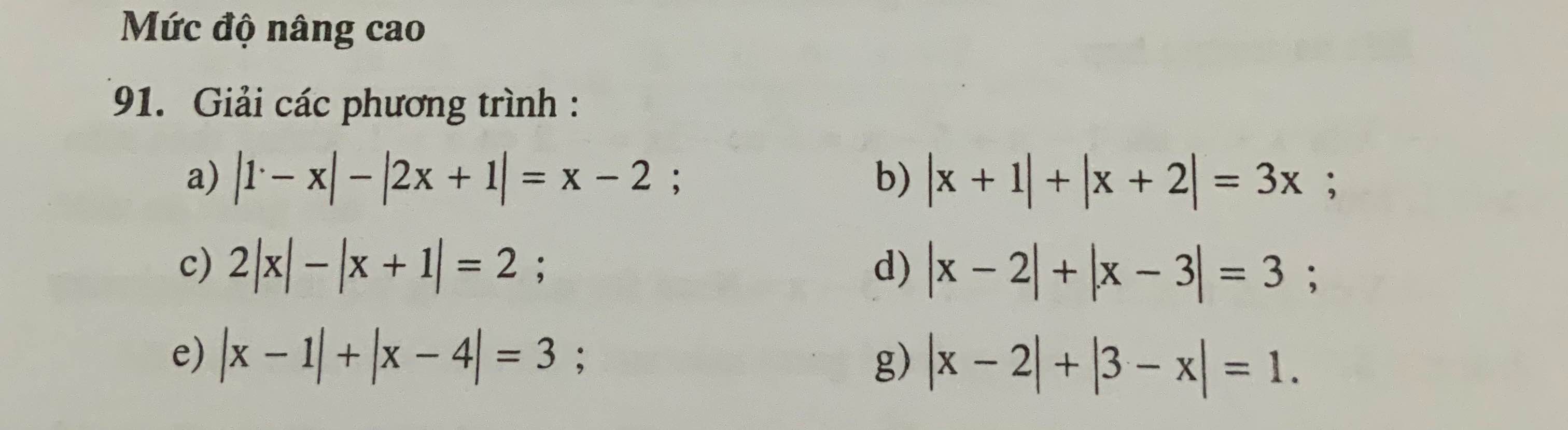Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bảng xét dấu :
| \(x\) | \(\frac{1}{2}\) \(1\) |
| \(1-x\) | \(-\) \(|\) \(-\) \(0\) \(+\) |
| \(2x-1\) | \(-\) \(0\) \(+\) \(|\) \(+\) |



x+2x−2−1x=2x(x−2)x+2x−2−1x=2x(x−2)
⇔x(x+2)x(x−2)−x−2x(x−2)=2x(x−2)⇔x(x+2)x(x−2)−x−2x(x−2)=2x(x−2)
⇔x2+2x−x+2−2=0⇔x2+2x−x+2−2=0
⇔x2+x=0⇔x2+x=0
⇔x(x+1)=0⇔[x=−1x=0

a: |1-x|-|2x+1|=x-2
=>|x-1|-|2x+1|=x-2(1)
TH1: x<-1/2
Phương trình (1) sẽ tương đương với:
1-x-(-2x-1)=x-2
=>1-x+2x+1=x-2
=>x+2=x-2
=>2=-2(vô lý)
=>\(x\in\varnothing\)
TH2: \(-\dfrac{1}{2}< =x< 1\)
Phương trình (1) sẽ trở thành:
\(1-x-\left(2x+1\right)=x-2\)
=>1-x-2x-1=x-2
=>-3x=x-2
=>-4x=-2
=>\(x=\dfrac{1}{2}\left(nhận\right)\)
TH3: x>=1
Phương trình (1) sẽ trở thành:
\(x-1-\left(2x+1\right)=x-2\)
=>x-1-2x-1=x-2
=>-x-2=x-2
=>-2x=0
=>x=0(loại)
b: \(\left|x+1\right|+\left|x+2\right|=3x\left(2\right)\)
TH1: x<-2
Phương trình (2) sẽ trở thành:
-x-1+(-x-2)=3x
=>\(3x=-2x-3\)
=>\(5x=-3\)
=>\(x=-\dfrac{3}{5}\left(loại\right)\)
TH2: -2<=x<-1
Phương trình (2) sẽ trở thành:
\(-x-1+x+2=3x\)
=>3x=1
=>\(x=\dfrac{1}{3}\left(loại\right)\)
TH3: x>=-1
Phương trình (2) sẽ trở thành:
\(x+1+x+2=3x\)
=>3x=2x+3
=>x=3(nhận)
c: \(2\left|x\right|-\left|x+1\right|=2\left(3\right)\)
TH1: x<-1
Phương trình (3) sẽ trở thành:
-2x-(-x-1)=2
=>-2x+x+1=2
=>-x+1=2
=>-x=1
=>x=-1(loại)
TH2: -1<=x<0
Phương trình (3) sẽ trở thành:
\(-2x-\left(x+1\right)=2\)
=>-2x-x-1=2
=>-3x=3
=>x=-1(nhận)
TH3: x>=0
Phương trình (3) sẽ trở thành:
\(2x-\left(x+1\right)=2\)
=>x-1=2
=>x=3(nhận)
d: \(\left|x-2\right|+\left|x-3\right|=3\left(4\right)\)
TH1: x<2
Phương trình (4) sẽ trở thành:
2-x+3-x=3
=>5-2x=3
=>2x=2
=>x=1(nhận)
Th2: 2<=x<3
Phương trình (4) sẽ trở thành:
\(x-2+3-x=3\)
=>1=3(loại)
Th3: x>=3
Phương trình (4) sẽ trở thành:
x-2+x-3=3
=>2x-5=3
=>2x=8
=>x=4(nhận)
e: |x-1|+|x-4|=3(5)
TH1: x<1
Phương trình (5) sẽ trở thành:
1-x+4-x=3
=>5-2x=3
=>2x=2
=>x=1(loại)
TH2: 1<=x<4
Phương trình (5) sẽ trở thành:
x-1+4-x=3
=>3=3(luôn đúng)
TH3: x>=4
Phương trình (5) sẽ trở thành:
x-1+x-4=3
=>2x-5=3
=>2x=8
=>x=4(nhận)
g: |x-2|+|3-x|=1
=>|x-2|+|x-3|=1(6)
TH1: x<2
Phương trình (6) sẽ trở thành:
2-x+3-x=1
=>5-2x=1
=>2x=4
=>x=2(loại)
TH2: 2<=x<3
Phương trình (6) sẽ trở thành:
x-2+3-x=1
=>1=1(luôn đúng)
TH3: x>=3
Phương trình (6) sẽ trở thành:
x-2+x-3=1
=>2x-5=1
=>2x=6
=>x=3(nhận)

/x-1/+x-2/=1 (1)
Bảng xét dấu:
| x | 1 | 2 | ||
| x-1 | -0 | + | bạn kéo 1 gạch đứng | + |
| x-2 | - bạn kéo 1 gạch đứng nha! | - | 0 | + |
TH1: x<1 thì (1) <=> 1-x+2-x=1
-2x + 3 = 1
- 2x = -1
x = 1 (KTM)
TH2:với 1< hoặc = x bé hơn hoặc = 2 thì ta có:
(1) <=> x-1+2-x=1
0x + 1 = 1
0x = 0 ( vô lý ) => (KTM)
TH3: với x>2 thì ta có:
(1) <=> x-1+x-2=1
2x -3 = 1
2x = 4
x = 2
vậy k có giá trị nào thỏa mãn
\(\Leftrightarrow|^{ }_{ }x-1|^{ }_{ }+|^{ }_{ }2-x|^{ }_{ }=1\)
co \(|^{ }_{ }x-1|^{ }_{ }\ge x-1\)voi moi x
\(|^{ }_{ }2-x|^{ }_{ }\ge2-x\)voi moi x
\(\Rightarrow|^{ }_{ }x-1|^{ }_{ }+|^{ }_{ }2-x|^{ }_{ }\ge x-1+2-x=1\)
dau bang xay ra \(\Leftrightarrow\hept{\begin{cases}x-1\ge0\\2-x\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge1\\x\le2\end{cases}}\Leftrightarrow1\le x\le2\)