QA
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 8 2019
gọi số cần tìm là abcdef
a có 4 cách chọn
+ với a = { 1,2,3}
b có 5 cách chọn
c có 4 cách chọn
d có 3 cách chọn
e có 2 cách chọn
f có 1 cách chọn
\(\Rightarrow\) có 360 số
+ với a = 4
b có 3 cách chọn
b={ 1,2}
c có 4 cách chọn
d có́ 3 cách chọn
e có 2 cách choṇ
f có 1 cách chọn
b =3
c có 1 cách chọn
d có 3 cách chọn
e có 2 cách chọn
f có 1 cách chọn
\(\Rightarrow\)có 54 số
vậy có 360 + 54 = 414 số
CM
31 tháng 7 2018
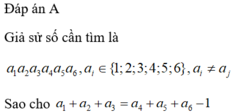
Vậy số cách để lập số có 6 chữ số khác nhau sao cho tổng ba số đầu nhỏ hơn tổng ba số cuối một đơn vị là: 
QA
3
DT
1
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
Gọi số cần lập là \(\overline{abcd}\)
TH1: \(a=1\)
\(\Rightarrow\) Bộ bcd có \(A_6^3=120\) số
TH2: \(a=2\Rightarrow b=0\) \(\Rightarrow c=1\)
d có 4 cách chọn \(\Rightarrow4\) số
\(\Rightarrow120+4=124\) số
NB
Từ các chữ số A= {0,1,2,3,5,6,8,9} có thể lập được bao nhiêu số tự nhiên khác nhau và nhỏ hơn 526??!
1
30 tháng 11 2021
Gọi các số cần tìm có dạng tổng quát là abc
Dựa vào các chữ số, lập được:
a có 3 cách chọn chữ số hàng trăm vì 0<a<5 => a= {1;2;3}
b có 8 cách chọn chữ số hàng chục - tất cả các số trên đều có đủ điều kiện để là c/s hàng chục
c có 8 cách chọn chữ số hàng đơn vị - tất cả các số trên đều có đủ điều kiện để là c/s hàng đơn vị
Bạn lập như thế với các số có dạng 5ab với a<2 và b<6 nhé!
=> Lập được các số để thỏa mãn ycđb là: 3x8x8+?= ? số
_HT_
20 tháng 8 2021
a) TH1 : Xét số thỏa yêu cầu kể cả chữ số đầu tiên bên trái =0
Chọn 3 chữ số lẻ có C35 cách
Chọn 3 chữ số chẵn có C35 cách
Sắp xếp 6 chữ số này có 6! cách
Vậy có C35 . C35 . 6! số
TH2 : Xét số có 6 chữ số thỏa mãn mà chữ số đầu tiên bên trái =0
Chọn 3 chữ số lẻ có C35 cách
Chọn 2 chữ số chẵn có C24 cách
Sắp xếp 5 chữ số có 5! cách
Vậy có C35 . C24 . 5! số
Vậy có C35 .C35. 6! - C35.C24.5! số tự nhiên gồm 6 chữ số khác nhau trong đó có 3 chữ số chẵn 3 chữ số lẻ
Nguyễn Việt Lâm
Nguyễn Việt Lâm