Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow\left(5m-2\right)x\le2m^2-m+2\)
- Với \(m=\frac{2}{5}\Rightarrow BPT\) đúng với mọi x \(\Rightarrow\) loại
- Với \(m< \frac{2}{5}\Rightarrow x\ge\frac{2m^2-m+2}{5m-2}\) \(\Rightarrow\) không tồn tại GTLN của x (loại)
- Với \(m>\frac{2}{5}\Rightarrow x\le\frac{2m^2-m+2}{5m-2}\)
Để BPT nhận nghiệm nguyên lớn nhất bằng 1
\(\Rightarrow\frac{2m^2-m+2}{5m-2}< 2\)
\(\Leftrightarrow2m^2-m+2< 10m-4\)
\(\Leftrightarrow2m^2-11m+6< 0\)
\(\Rightarrow\frac{11-\sqrt{73}}{4}< m< \frac{11+\sqrt{73}}{4}\)
\(\Rightarrow m=\left\{1;2;3;4\right\}\)

\(mx^2-2\left(m+2\right)x+2m-1< 0\)
\(< =>mx^2-2\left(m+2\right)x+2m-1\ge0\)
\(a=m\ne0\)
\(\Delta=\left(2m+2\right)^2-4m\left(2m-1\right)\)
\(\Delta=4m^2+8m+4-8m^2+4m\)
\(\Delta=12m-4m^2+4\)
\(< =>\hept{\begin{cases}a>0\\\Delta\le0\end{cases}\hept{\begin{cases}m>0\\12m-4m^2+4\le0\end{cases}\hept{\begin{cases}m>0\\m=\left[\frac{3-\sqrt{13}}{2};\frac{3+\sqrt{13}}{2}\right]\end{cases}}}}\)
\(< =>m=(0;\frac{3+\sqrt{13}}{2}]\)
vậy m vô số nghiệm để bpt vô nghiệm

Ta có: D = 2 m + 1 1 m 2 − 1 = − 2 m − 1 − m 2 = − m + 1 2
D x = 2 m − 2 1 m 2 − 3 m − 1
= − 2 m + 2 − m 2 + 3 m = − m 2 + m + 2 = m + 1 2 − m
D y = 2 m + 1 2 m − 2 m 2 m 2 − 3 m = 2 m + 1 m 2 − 3 m − m 2 2 m − 2
= − 3 m 2 − 3 m = − 3 m m + 1
Nếu m ≠ − 1 thì hệ phương trình có nghiệm duy nhất
x = D x D = m − 2 m + 1 = 1 − 3 m + 1 y = D y D = 3 m m + 1 = 3 − 3 m + 1
Để x , y ∈ Z suy ra 3 m + 1 ∈ Z , m + 1 ∈ U , ( 3 ) = ± 1 ; ± 3
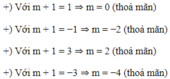
Vậy có 4 giá trị của m thoả mãn đề bài.
Đáp án cần chọn là: D