K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
30 tháng 4 2017
Chọn B
Số phần tử không gian mẫu là số cách chia 8 đội bóng vào hai bảng sao cho mỗi bảng có 4 đội
Gọi A là biến cố thỏa mãn yêu cầu bài toán.
Ta có: 
5 tháng 1 2021
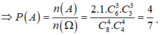
\(A^3_n+5A^2_n=2\left(n+15\right)\)
ĐK: n ≥ 3 (n∈N)
<=> \(\dfrac{n!}{\left(n-3\right)!}+\dfrac{5.n!}{\left(n-2\right)!}=2\left(n+15\right)\)
<=> \(\dfrac{n\left(n-1\right)\left(n-2\right)\left(n-3\right)!}{\left(n-3\right)!}+\dfrac{5n\left(n-1\right)\left(n-2\right)!}{\left(n-2\right)!}=2\left(n+15\right)\)
<=> \(n\left(n-1\right)\left(n-2\right)+5\left(n-1\right)n-2n-30=0\)
<=> \(n^3+2n^2-5n-30=0\) <=> n=3
K
20 tháng 5 2019
Bạn mk khen hok đc chứ mk hok Vinastudy, Vinastudy dạy cũng hay lắm bạn à.
6 tháng 11 2016
Chuyên đề [url=http://toancap3.com/chuyen-de/to-hop-va-nhi-thuc-newton/]tổ hợp và nhị thức newton[/url]
ko=)
em nghĩ là có đó chị :))