Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

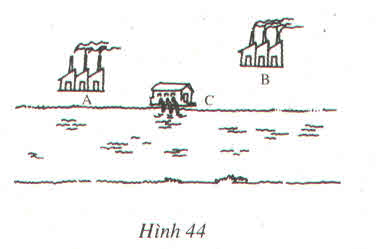
Câu 1: Người ta muốn mắc dây điện từ một trạm biến áp A đến một khu dân cư B được xây dựng nằm cách xa nhau tại hai bờ của một con sông d. Vị trí trên bờ sông để cắm cột mắc dây C sao cho số mét dây phải dùng là ngắn nhất là:
A. Vị trí cắm cột C là chân đường vuông góc hạ từ trạm biến áp A đến bờ sông d.
B. Vị trí cắm cột C là chân đường vuông góc hạ từ một vị trí B của khu dân cư đến bờ sông d.
C. Vị trí cắm cột C là giao điểm của AB và bờ sông d.
D. Vị trí cắm cột C bất kì trên bờ sông d.

Áp dụng bài 48
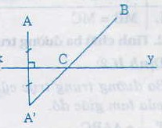
Gọi A' là điểm đối xứng của A qua đường thẳng xy chứa một bờ sông gần nhất
Ta có: CA + CB = CA' + CB ≥ A'B
Nên CA + CB ngắn nhất khi C là giao điểm của A'B với xy
Vậy điểm đặt trạm bơm là giao điểm của đường thẳng xy với đường thẳng qua điểm B và điểm A' đói xứng với A qua xy.
Áp dụng bài 48

Gọi A' là điểm đối xứng của A qua đường thẳng xy chứa một bờ sông gần nhất
Ta có: CA + CB = CA' + CB ≥ A'B
Nên CA + CB ngắn nhất khi C là giao điểm của A'B với xy
Vậy điểm đặt trạm bơm là giao điểm của đường thẳng xy với đường thẳng qua điểm B và điểm A' đói xứng với A qua xy.

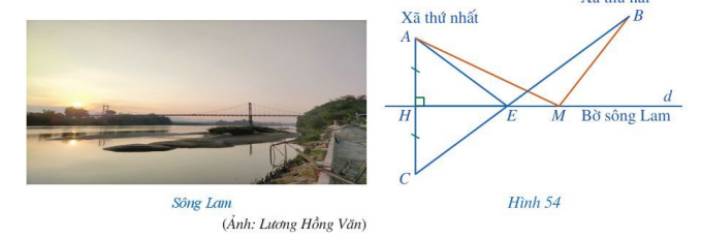
Ta có: HA = HC, \(EH \bot AC\). Vậy EH là đường trung trực của AC nên EA = EC (tính chất đường trung trực của đoạn thẳng).
Tương tự ta có: MH là đường trung trực của AC nên MA = MC.
Xét tam giác MBC: \(BC < MB + MC\)(Trong một tam giác, tổng của hai cạnh luôn lớn hơn độ dài cạnh còn lại).
Ta có:
\(BC < MB + MC = MB + MA\). (1)
Ba điểm B, E, C thẳng hàng nên \(EB + EC = BC\). (2)
Thay (2) vào (1) ta được: \(\begin{array}{l}BC < MB + MA\\EB + EC < MA + MB\end{array}\)
Mà EA = EC nên \(EA + EB < MA + MB\). Vậy bạn Nam nói đúng và khi đó để tổng khoảng cách từ hai xã đến chân cầu là nhỏ nhất thì E là vị trí của cây cầu.

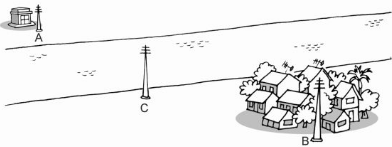
Gọi đường thẳng xy là bờ sông cần xây trạm bơm.
⇒ Bài toán đưa về: Hai điểm A, B cố định cùng nằm trên nửa mặt phẳng bờ là đường thẳng xy. Tìm vị trí điểm C nằm trên đường xy sao cho CA + CB nhỏ nhất.
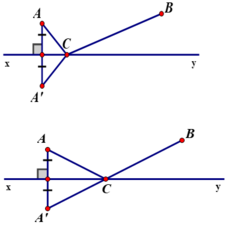
Gọi A’ là điểm đối xứng của A qua đường thẳng xy.
Theo như chứng minh ở bài 48 ta có: CA + CB = CA’ + CB ≥ A’B (A’B cố định).
⇒ CA + CB đạt ngắn nhất bằng A’B.
Dấu “=” xảy ra khi CA’+CB = A’B, tức là A’; B; C thẳng hàng hay C là giao điểm của A’B và xy.
Vậy điểm đặt trạm bơm là giao điểm của đường thẳng xy với đường thẳng A’B, trong đó A’ là điểm đối xứng với A qua xy.

Gọi đường thẳng xy là bờ sông cần xây trạm bơm.
⇒ Bài toán đưa về: Hai điểm A, B cố định cùng nằm trên nửa mặt phẳng bờ là đường thẳng xy. Tìm vị trí điểm C nằm trên đường xy sao cho CA + CB nhỏ nhất.
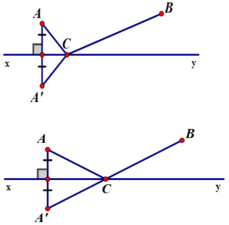
Gọi A’ là điểm đối xứng của A qua đường thẳng xy.
Theo như chứng minh ở bài 48 ta có: CA + CB = CA’ + CB ≥ A’B (A’B cố định).
⇒ CA + CB đạt ngắn nhất bằng A’B.
Dấu “=” xảy ra khi CA’+CB = A’B, tức là A’; B; C thẳng hàng hay C là giao điểm của A’B và xy.
Vậy điểm đặt trạm bơm là giao điểm của đường thẳng xy với đường thẳng A’B, trong đó A’ là điểm đối xứng với A qua xy.

Ta có:
\(AC+BC\ge AB\) ( vì \(C\)là điểm chưa xác định )
Do đó:
\(AC+BC\)ngắn nhất khi:
\(AC+BC=AB\)
\(\Rightarrow C\)nằm giữa \(AB\)
Vậy vị trí đặt một cột mắc dây điện từ trạm về cho khu dân cư sao cho độ dài đường dây ngắn nhất là \(C\)nằm giữa \(AB\)
Ta có: AC + BC ≥ AB ( vì C là điểm chưa xác định)
Do đó : AC + BC ngắn nhất khi:
AC + BC = AB
=> C nằm giữa A và B
Vậy vị trí đặt một cột mắc dây điện từ trạm về cho khu dân cư sao cho độ dài đường dây dẫn ngắn nhất là C nằm giữa A và B