
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(17^{19}+19^{17}=\left(17^{19}+1\right)+\left(19^{17}-1\right)\)
Mà \(17^{19}+1\)chia hết cho \(17+1=18\)
và \(19^{17}-1\)chia hết cho \(19-1=18\)
nên \(\left(17^{19}+1\right)+\left(19^{17}-1\right)\)chia hết cho \(18\)
Do đó, \(17^{19}+19^{17}\)chia hết cho \(18\)


c) 17^19 + 19^17 = (17^19 + 1) + (19^17
- 1)
17^19 + 1 chia hết cho 17 + 1 = 18 và 19^17
- 1 chia hết cho 19 - 1 = 18 nên (17^19 + 1) + (19^17
- 1)
hay 17^19 + 19^17 chia hết cho 18

a) Ta áp dụng đẳng thức sau: \(a^{2k+1}+b^{2k+1}⋮a+b\)
\(A=2^{70}+b^{70}=4^{35}+9^{35}⋮4+9=13\)
\(\Rightarrowđpcm\)
b) Ta có: \(17\equiv-1\left(mod18\right)\Rightarrow17^{19}\equiv-1\left(mod18\right)\)
\(19\equiv1\left(mod18\right)\Rightarrow19^{17}\equiv1\left(mod18\right)\)
\(\Rightarrow17^{19}+19^{17}⋮18\left(đpcm\right)\)

a) Có: \(2^3=8\equiv1\left(mod7\right)\Rightarrow2^{51}\equiv1\left(mod7\right)\)
\(\Rightarrow2^{51}-1⋮7\left(đpcm\right)\)
b) 270 + 370 = (22)35 + (32)35 = 435 + 935
\(=\left(4+9\right).\left(4^{34}-4^{33}.9+....-4.9^{33}+9^{34}\right)\)
\(=13.\left(4^{34}-4^{33}.9+...-4.9^{33}+9^{34}\right)⋮13\left(đpcm\right)\)

Bạn ơi, mik mới học lớp 8 thôi, bạn giải dùng nhiều kí tự mik ko hiểu, bạn có cách khác ko, hiện tại mik chỉ mới học hằng đẳng thức thôi ạ. Nhưng vẫn cảm ơn bạn rất nhiều bạn nha.

a)Đặt \(A=8^5+2^{11}\)
\(A=\left(2^3\right)^5+2^{11}\)
\(A=2^{15}+2^{11}\)
\(A=2^{11}\left(2^4+1\right)\)
\(A=2^{11}\cdot17⋮17\left(đpcm\right)\)

phần a sai đề nha bạn
b,Ta có
\(2\equiv2\left(mod13\right)\)
\(\Rightarrow2^{12}\equiv1\left(mod13\right)\)
\(\Rightarrow2^{12.5}.2^{10}\equiv1.2^{10}\left(mod13\right)\)
\(\Rightarrow2^{60}.2^{10}\equiv1024\left(mod13\right)\)
\(\Rightarrow2^{70}\equiv10\left(mod13\right)\)\(\left(1\right)\)
Lại có:
\(3\equiv3\left(mod13\right)\)
\(\Rightarrow3^6\equiv1\left(mod13\right)\)
\(\Rightarrow3^{6.11}.3^4\equiv1.3^4\left(mod13\right)\)
\(\Rightarrow3^{66}.3^4\equiv81\left(mod13\right)\)
\(\Rightarrow3^{70}\equiv3\left(mod13\right)\)\(\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow2^{70}+3^{70}\equiv13\equiv0\left(mod13\right)\)
c, Ta có
\(17\equiv-1\left(mod18\right)\)
\(\Rightarrow17^{19}\equiv-1\left(mod18\right)\)\(\left(1\right)\)
Lại có
\(19\equiv1\left(mod18\right)\)
\(\Rightarrow19^{17}\equiv1\left(mod18\right)\)\(\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow17^{19}+19^{17}\equiv0\left(mod18\right)\)
\(\Rightarrow17^{19}+19^{17}⋮18\)
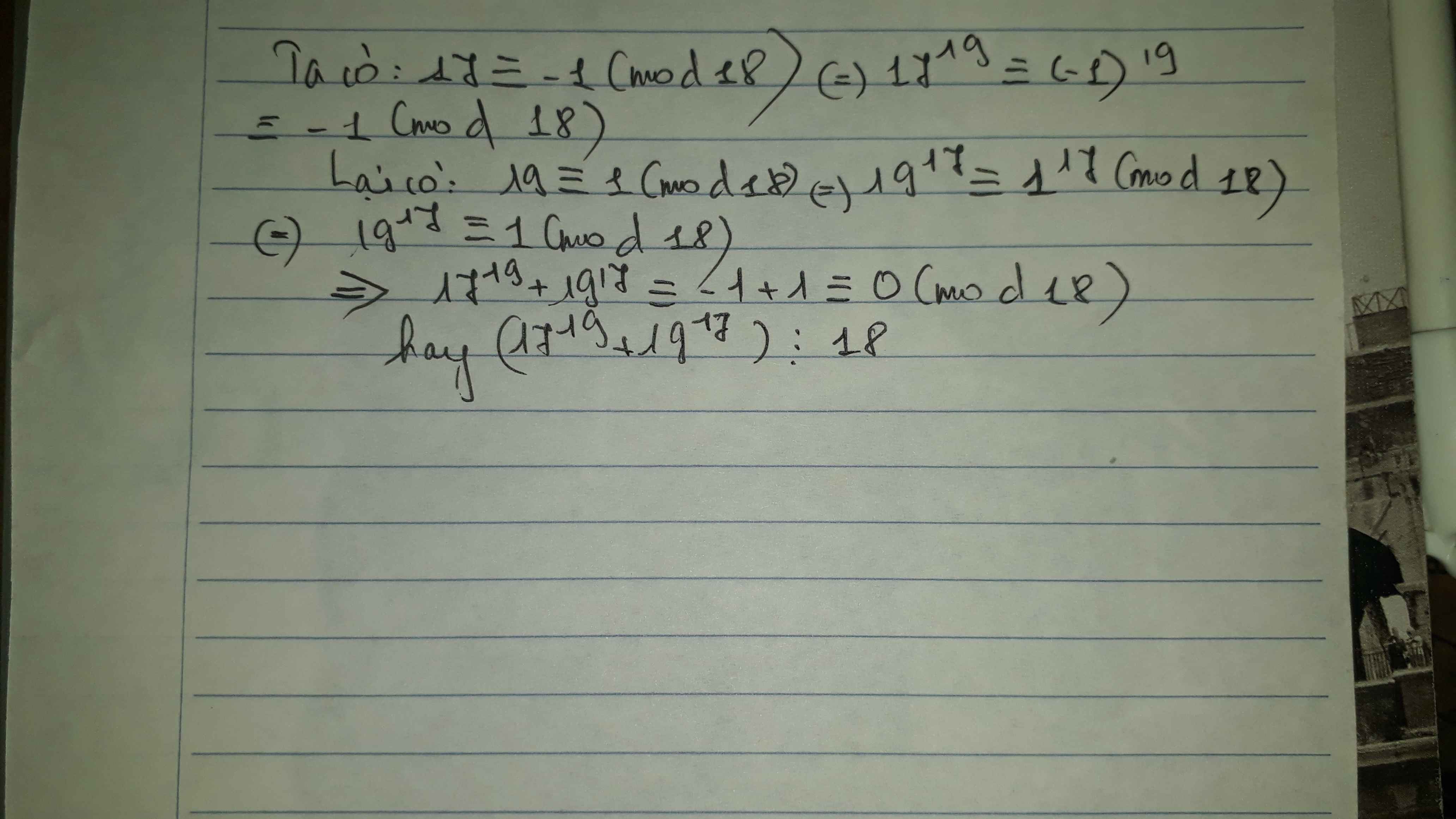
Ta có: 1719 + 1917 = (1719 + 1) + (1917 - 1)
\(17^{19}+1⋮17+1=18\)
và \(19^{17}-1⋮19-1=18\)
nên (1719+1)+(1917-1) hay 1719+1917 chia hết cho 18
Giúp mik vs cb