
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi x0y và y0z là hai góc kề bù , ot là pg x0y ; 0t' là p/g của y0z
Ta có
y0t = 1/2 x0y ( ot là p/g) (1)
y0t' = 1/2 y0x ( 0t' là p/g) (2)
x0y + y0z = 180 độ ( kề bù)
Từ (1) và (2) => y0t + yot' = 1/2 ( xoy+ y0z) = 1/2 .180 = 9 0 độ
=> t0t' = 90 đọ
hay 0t vuông góc với 0t' => ĐPCM

B O C A N M
Cho góc AOB và góc BOC là hai góc kề bù , OM , ON lần lượt là các ia phân giác của góc ACB và góc BOC
Chứng minh góc MON = 90 độ
Ta có : OM là tia phân giác của góc AOB nên tia OM nằm giữa hai tia OA và OB và góc MOB = 1/2 góc AOB
Tương tự : ON là tia pân giác của góc BOC nên ON nằm giữa hai tia OB và OC và góc BON = 1/2 góc BOC
Lại có : góc AOB và góc BOC là hai góc kề bù nên tia OB nằm giữa hai tia OA va OC
Suy ra : OB nằm giữa hai tia OM và ON nên :
góc MON = góc MOB + góc BON
= 1/2 * ( góc AOB + góc BOC )
= 1/2 * 180 độ = 90 độ
Cho góc AOB và góc BOC là hai góc kề bù , OM , ON lần lượt là các ia phân giác của góc ACB và góc BOC Chứng minh góc MON = 90 độ Ta có : OM là tia phân giác của góc AOB nên tia OM nằm giữa hai tia OA và OB và góc MOB = 1/2 góc AOB Tương tự : ON là tia pân giác của góc BOC nên ON nằm giữa hai tia OB và OC và góc BON = 1/2 góc BOC Lại có : góc AOB và góc BOC là hai góc kề bù nên tia OB nằm giữa hai tia OA va OC Suy ra : OB nằm giữa hai tia OM và ON nên : góc MON = góc MOB + góc BON = 1/2 * ( góc AOB + góc BOC ) = 1/2 * 180 độ = 90 độ

Xét Om và On thứ tự là tia phân giác của hai góc kề bù x O z ^ và z O y ^ . Ta có: x O z ^ + z O y ^ = 180 0 (hai góc kề bù) Mà Om là tia phân giác của x O z ^ => x O z ^ = 2 m O z ^ On là tia phân giác của z O y ^ ⇒ z O y ^ = 2 n O z ^ |
|
Do đó: 2 m O z ^ + 2 n O z ^ = 180 0
⇒ m O z ^ + n O z ^ = 90 0
⇒ m O n ^ = 90 0 ⇒ O m ⊥ O n
Vậy hai tia phân giác của hai góc kề bù thì vuông góc với nhau
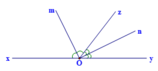

* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.

Tham khảo link này nhé ^^
https://h7.net/hoi-dap/toan-7/hai-tia-phan-giac-cua-hai-goc-ke-bu-vuong-goc-voi-nhau-faq25757.html

\(Góc\)\(kề\)\(bù\)\(có\)\(số\)\(đo=90^0\)
\(2\)\(góc\)\(kề\)\(bù\)\(\Rightarrow mỗi\)\(góc=90^0\)
\(Tia\)\(phân\)\(giác\)\(của\)\(1\)\(góc\)\(kề\)\(bù=90^0:2=45^0\)
\(\Rightarrow Tia\)\(phân\)\(giác\)\(của\)\(2\)\(góc\)\(kề\)\(bù=45^0+45^0=90^0\)
thấy: xOy + yOz = 1800
=>1/2 xOy + 1/2 yOz = 1/2(xOy+yOz)=1/2 xOz=1/2 x 180 dộ
=90 độ
Vậy hai tia phân giác của 2 góc kề bù thì vuông góc với nhau
xOzy

O m n p e f 1 2 3 4
Giải :
Ta có: \(\widehat{mOn}+\widehat{nOp}=180^0\)
=> \(\widehat{O_1}+\widehat{O_2}+\widehat{O_3}+\widehat{O_4}=180^0\)
=> \(\widehat{O_1}+\widehat{O_4}+90^0=180^0\) (vì Of \(\perp\)Oe => \(\widehat{fOe}=\widehat{O_2}+\widehat{O_3}=90^0\))
=> \(\widehat{O_1}+\widehat{O_4}=90^0\) (1)
Do \(\widehat{O_1}=\widehat{O_2}\) (gt) => \(\widehat{O_1}+\widehat{O_3}=90^0\) (2)
Từ (1) và (2) => \(\widehat{O_3}=\widehat{O_4}\)
Mà Of nằm giữa \(\widehat{nOp}\)
=> Of là tia p/giác của \(\widehat{nOp}\)