
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi góc A' ; B' ; C' ; D' là góc ngoài của đỉnh A ; B ; C : D
Ta có A + A' =180 ( kề bù )
B + B' = 180
C + C' = 180
D + D' = 180
Suy ra : A + A' + B + B' + C + C' + D + D' = 180 + 180 + 180 + 180
360 + A' + B' + C' + D' = 720 ( tứ giác ABCD nên tổng 4 góc A ; B ; C ; D = 360 )
A' + B' + C' + D' = 360

gọi các góc trong của đỉnh A và C là ^A1 và ^C1
còn các góc ngoài của đỉnh A và C là ^A2 và ^C2
ta có ^A1 + ^A2 =180o ( 2 góc kè bù )
và ^C1 +^C2 =180o (2 góc kề bù )
=> ^A2 =180o -^A1
và ^C2 =180o -^C2
=> ^A2+^C2 = 360o -^A1-^C1(1)
ta lại có ^A1+^B+^C1+^D =360o (tổng 4 góc tứ giác )
=> ^B+^D = 360o - ^A1-^C1(2)
từ (1) và(2) => ^B+^D = ^A2 +^C2 (cùng = 3600 -^a1 -^C1)
vậy.............

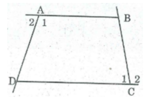
* Gọi ∠ A 1 , ∠ C 1 là góc trong của tứ giác tại đỉnh A và C, ∠ A 2 , ∠ C 2 là góc ngoài tại đỉnh A và C.
Ta có: ∠ A 1 + ∠ A 2 = 180 0 (2 góc kề bù)
⇒ ∠ A 2 = 180 0 - ∠ A 1
∠ C 1 + ∠ C 2 = 180 0 (2 góc kề bù) ⇒ ∠ C 2 = 180 0 - ∠ C 1
Suy ra: ∠ A 2 + ∠ C 2 = 180 0 - ∠ A 1 + 180o - ∠ C 1 = 360 0 – ( ∠ A 1 + ∠ C 1 ) (1)
* Trong tứ giác ABCD ta có:
∠ A 1 + ∠ B + ∠ C 1 + ∠ D = 360 0 (tổng các góc của tứ giác)
⇒ ∠ B + ∠ D = 360 0 - ( ∠ A 1 + ∠ C 1 ) (2)
Từ (1) và (2) suy ra: ∠ A 2 + ∠ C 2 = ∠ B + ∠ D


Tổng của góc trong và góc ngoài đỉnh A là \(180^o\) (2 góc kề bù)
Tương tự với các đỉnh B;C;D
Tổng của góc trong và góc ngoài tại 4 đỉnh là \(180^o\cdot4=720^o\)
Mà tổng 4 góc trong tứ giác là \(360^o\)
Nên tổng 4 góc ngoài của tứ giác là \(720^o-360^o=360^o\)