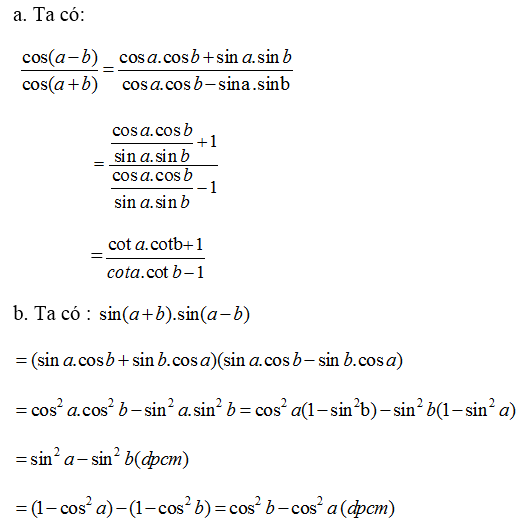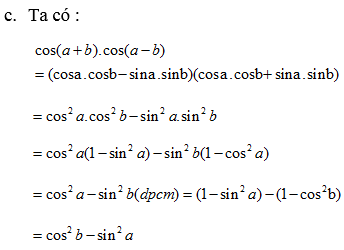Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
\(\sin (a+b)=\sin (a+b+c-c)=\sin (a+b+c).\cos c-\cos (a+b+c)\sin c\)
\(\sin (a+c)=\sin (a+c+b-b)=\sin (a+b+c)\cos b-\cos (a+b+c)\sin b\)
Do đó:
\(\text{VT}=\sin (a+b+c)\cos b\cos c-\cos (a+b+c)\sin c\cos b-\sin (a+b+c)\cos b\cos c+\cos (a+b+c)\sin b\cos c\)
\(=\sin (a+b+c)(\cos b\cos c-\cos b\cos c)+\cos (a+b+c)(\sin b\cos c-\sin c\cos b)\)
\(=\cos (a+b+c)(\sin b\cos c-\cos b\sin c)=\cos (a+b+c)\sin (b-c)\)
\(=\text{VP}\)
Ta có đpcm.

a) \(sin\left(270^o-\alpha\right)=sin\left(-90^o-\alpha\right)=-sin\left(90^o+\alpha\right)\)\(=-cos\alpha\).
b) \(cos\left(270^o-\alpha\right)=cos\left(-90^o-\alpha\right)=cos\left(90^o+\alpha\right)\)\(=-sin\alpha\).
c) \(sin\left(270^o+\alpha\right)=sin\left(-90^o+\alpha\right)=-sin\left(90^o-\alpha\right)\)\(=-cos\alpha\).
d) \(cos\left(270^o+\alpha\right)=cos\left(-90^o+\alpha\right)=cos\left(90^o-\alpha\right)\)\(=sin\alpha\).

Mẫn Li
Câu 4 nếu bạn ko đánh sai thì người ghi đề sai :D, tử số phải là sinb chứ ko phải sina (đã chứng minh bên trên)
Câu 2b sửa lại thì cm dễ thôi:
\(\frac{cos\left(a+b\right).cos\left(a-b\right)}{sin^2a.sin^2b}=\frac{\frac{1}{2}cos2a+\frac{1}{2}cos2b}{sin^2a.sin^2b}=\frac{1-sin^2a-sin^2b}{sin^2a.sin^2b}=\frac{1}{sin^2a.sin^2b}-\frac{1}{sin^2a}-\frac{1}{sin^2b}\)
\(=\left(1+cot^2a\right)\left(1+cot^2b\right)-\left(1+cot^2a\right)-\left(1+cot^2b\right)\)
\(=1+cot^2a+cot^2b+cot^2a.cot^2b-2-cot^2a-cot^2b\)
\(=cot^2a.cot^2b-1\)
(từ đầu bằng thứ nhất ra thứ 2 sử dụng ct nhân đôi \(cos2x=1-2sin^2x\))
Rất xin lỗi bạn!
Câu 2b do mình đánh sai dấu phải là \(\frac{cos\left(a+b\right)\times cos\left(a-b\right)}{sin^2a\times sin^2b}=cot^2a\times cot^2b-1\)
Câu 3 mình cũng đánh sai luôn:
\(sin\frac{A}{2}=cos\frac{B}{2}\times cos\frac{C}{2}-sin\frac{C}{2}\times sin\frac{B}{2}\)
Còn câu 4 thì mình ko có đánh sai! Thành thật xin lỗi bạn! Mình sẽ khắc phục sự cố này!

\(\frac{cos\left(a-b\right)}{sin\left(a+b\right)}=\frac{cosa.cosb+sina.sinb}{sina.cosb+cosa.sinb}=\frac{\frac{cosa.cosb}{sina.sinb}+1}{\frac{sina.cosb}{sina.sinb}+\frac{cosa.sinb}{sina.sinb}}=\frac{cota.cotb+1}{cota+cotb}\)
Bạn ghi đề ko đúng
\(sin\left(a+b\right)sin\left(a-b\right)=\frac{1}{2}\left[cos2b-cos2a\right]\)
\(=\frac{1}{2}\left[1-2sin^2b-1+2sin^2a\right]\)
\(=sin^2a-sin^2b\)
\(=1-cos^2a-1+cos^2b=cos^2b-cos^2a\)
Câu này bạn cũng ghi đề ko đúng
\(cos\left(a+b\right)cos\left(a-b\right)=\frac{1}{2}\left[cos2a+cos2b\right]\)
\(=\frac{1}{2}\left[2cos^2a-1+1-2sin^2b\right]=cos^2a-sin^2b\)
\(=1-sin^2a-1+cos^2b=cos^2b-sin^2a\)

a) \(A=2\left(sin^6\alpha+cos^6\alpha\right)-3\left(sin^4\alpha+cos^4\alpha\right)\)
\(=2\left(sin^2\alpha+cos^2\alpha\right)\left(sin^4\alpha-sin^2\alpha cos^2\alpha+cos^4\alpha\right)\)\(-3\left(sin^4\alpha+cos^4\alpha\right)\)
\(=2\left(sin^4\alpha+cos^4\alpha-sin^2\alpha cos^2\alpha\right)-3\left(sin^4\alpha+cos^4\alpha\right)\)
\(=-\left(sin^4\alpha+cos^4\alpha+2sin^2\alpha cos^2\alpha\right)\)
\(=-\left(sin^2\alpha+cos^2\alpha\right)^2=-1\) (Không phụ thuộc vào \(\alpha\)).
b) \(B=4\left(sin^4\alpha+cos^4\alpha\right)-cos4\alpha\)
\(=4\left(sin^4\alpha+cos^4\alpha+2sin^2\alpha cos^2\alpha\right)-8sin^2\alpha cos^2\alpha\)\(-\left(1-2sin^22\alpha\right)\)
\(=4.\left(sin^2\alpha+cos^2\alpha\right)^2-2sin^22\alpha-1+2sin^22\alpha\)
\(=4-1=3\).

\(A=cosa\left(sinb.cosc-cosb.sinc\right)+cosb\left(sinc.cosa-cosc.sina\right)+cosc\left(sinacosb-cosasinb\right)\)
\(A=cosasinbcosc-cosacosbsinc+cosacosbsinc-sinacosbcosc+sinacosbcosc-cosasinbcosc\)
\(A=0\)
\(B=sin^2x+\frac{1}{2}\left(cos\frac{2\pi}{3}+cos2x\right)\)
\(B=\frac{1}{2}-\frac{1}{2}cos2x-\frac{1}{4}+\frac{1}{2}cos2x\)
\(B=\frac{1}{4}\)
\(C=\frac{1}{2}-\frac{1}{2}cos2x+\frac{1}{2}-\frac{1}{2}cos\left(\frac{4\pi}{3}+2x\right)+\frac{1}{2}-\frac{1}{2}cos\left(\frac{4\pi}{3}-2x\right)\)
\(C=\frac{3}{2}-\frac{1}{2}cos2x-\frac{1}{2}\left(cos\left(\frac{4\pi}{3}+2x\right)+cos\left(\frac{4\pi}{3}-2x\right)\right)\)
\(C=\frac{3}{2}-\frac{1}{2}cos2x-cos\frac{4\pi}{3}.cos2x\)
\(C=\frac{3}{2}-\frac{1}{2}cos2x+\frac{1}{2}cos2x\)
\(C=\frac{3}{2}\)
\(D=\frac{1}{2}\left[\sqrt{2}sin\left(\frac{\pi}{4}+x\right)\right]^2-sin^2x-sinx.\sqrt{2}cos\left(\frac{\pi}{4}+x\right)\)
\(D=\frac{1}{2}\left(sinx+cosx\right)^2-sin^2x-sinx\left(sinx-cosx\right)\)
\(D=\frac{1}{2}\left(1+2sinx.cosx\right)-sin^2x-sin^2x+sinx.cosx\)
\(D=\frac{1}{2}+sinxcosx+sinxcosx=\frac{1}{2}+sin2x\)
Góc độ cao của thang dựa vào tường là 60º và chân thang cách tường 4,6 m. Chiều dài của thang là

\(VT=\dfrac{1+2cos^2\dfrac{a}{2}-1-2sin\dfrac{a}{2}cos\dfrac{a}{2}}{1-\left(1-2sin^2\dfrac{a}{2}\right)-2sin\dfrac{a}{2}cos\dfrac{a}{2}}=\dfrac{2cos^2\dfrac{a}{2}-2sin\dfrac{a}{2}cos\dfrac{a}{2}}{2sin^2\dfrac{a}{2}-2sin\dfrac{a}{2}cos\dfrac{a}{2}}\)
\(=\dfrac{2cos\dfrac{a}{2}\left(cos\dfrac{a}{2}-sin\dfrac{a}{2}\right)}{2sin\dfrac{a}{2}\left(sin\dfrac{a}{2}-cos\dfrac{a}{2}\right)}\)
\(=-\dfrac{cos\dfrac{a}{2}}{sin\dfrac{a}{2}}=-cot\dfrac{a}{2}=VP\\ \Rightarrowđpcm\)