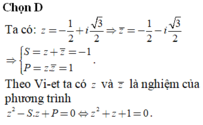Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu z = a + bi thì z + z = 2a ∈ R; z. z = a 2 + b 2 ∈ R
z và z là hai nghiệm của phương trình (x − z)(x − z ) = 0
⇔ x 2 − (z + z ) x + z. z = 0
⇔ x 2 − 2ax + a 2 + b 2 = 0

Nếu z = a + bi thì z + z = 2a ∈ R; z. z = a 2 + b 2 ∈ R
z và z là hai nghiệm của phương trình (x − z)(x − z ) = 0
⇔ x 2 − (z + z ) x + z. z = 0
⇔ x 2 − 2ax + a 2 + b 2 = 0

Một phương trình bậc hai nhận z và làm nghiệm là
(x - z)(x - ) = 0 hay x2 – (z +
)x + z
= 0.
Nếu z = a + bi thì z + = 2a, z
= a2 + b2
Vậy một phương trình bậc hai cần tìm là x2 – 2ax + a2 + b2 = 0

Đặt z1 + z2 = a; z1. z2 = b; a, b ∈ R
Khi đó, z1 và z2 là hai nghiệm của phương trình
(z – z1)(z – z2) = 0 hay z2 – (z1 + z2)z + z1. z2 = 0 ⇔ z2 – az + b = 0
Đó là phương trình bậc hai đối với hệ số thực. Suy ra điều phải chứng minh.
TRONG VONG MAY PHUT MA GIAI MẤY BÀI LIỀN BẠN LÀ 1 SIÊU NHÂN GIẢI TOÁN...HOẶC BẠN LÀ 1 SIÊU NHÂN SAO CHÉP TỪ SÁCH GIẢI BÀI TẬP LÊN ĐỂ CẦU ...."GP"![]()