
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
Đặt \(f\left(x\right)=\left(m^2+1\right)x^3-2m^2x^2-4x+m^2+1\)
\(f\left(x\right)\) xác định và liên tục trên R
\(f\left(x\right)\) có bậc 3 nên có tối đa 3 nghiệm (1)
\(f\left(0\right)=m^2+1>0\) ; \(\forall m\)
\(f\left(1\right)=\left(m^2+1\right)-2m^2-4+m^2+1=-2< 0\) ;\(\forall m\)
\(\Rightarrow f\left(0\right).f\left(1\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;1\right)\) (2)
\(f\left(2\right)=8\left(m^2+1\right)-8m^2-8+m^2+1=m^2+1>0\)
\(\Rightarrow f\left(1\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;2\right)\) (3)
\(f\left(-3\right)==-27\left(m^2+1\right)-18m^2+12+m^2+1=-44m^2-14< 0\)
\(\Rightarrow f\left(-3\right).f\left(0\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-3;0\right)\) (4)
Từ (1); (2); (3); (4) \(\Rightarrow f\left(x\right)=0\) có đúng 3 nghiệm phân biệt
2.
Đặt \(t=g\left(x\right)=x.cosx\)
\(g\left(x\right)\) liên tục trên R và có miền giá trị bằng R \(\Rightarrow t\in\left(-\infty;+\infty\right)\)
\(f\left(t\right)=t^3+m\left(t-1\right)\left(t+2\right)\)
Hàm \(f\left(t\right)\) xác định và liên tục trên R
\(f\left(1\right)=1>0\)
\(f\left(-2\right)=-8< 0\)
\(\Rightarrow f\left(1\right).f\left(-2\right)< 0\Rightarrow f\left(t\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(-2;1\right)\)
\(\Rightarrow f\left(x\right)=0\) luôn có nghiệm với mọi m

Đặt \(f\left(x\right)=\left(5-3m\right)x^7+m^2x^4-2\Rightarrow f\left(x\right)\) liên tục trên R
\(f\left(0\right)=-2< 0\)
\(f\left(1\right)=m^2-3m+3=\left(m-\dfrac{3}{2}\right)^2+\dfrac{3}{4}>0\) ;\(\forall m\)
\(\Rightarrow f\left(0\right).f\left(1\right)< 0\) ;\(\forall m\)
\(\Rightarrow f\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;1\right)\) (đpcm)

Xét hàm \(f\left(x\right)=m\left(x-1\right)^3\left(x^2-4\right)+x^4-3\)
Hàm \(f\left(x\right)\) là hàm liên tục trên R
\(f\left(1\right)=-2< 0\)
\(f\left(-2\right)=13>0\)
\(\Rightarrow f\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(-2;1\right)\)
\(f\left(2\right)=13>0\Rightarrow f\left(1\right).f\left(2\right)< 0\)
\(\Rightarrow f\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;2\right)\)
\(\Rightarrow\) Phương trình đã cho luôn có ít nhất 2 nghiệm với mọi m


a.
- Với \(m=\pm1\Rightarrow-6x=1\Rightarrow x=-\dfrac{1}{6}\) có nghiệm
Đặt \(f\left(x\right)=\left(1-m^2\right)x^3-6x-1\)
- Với \(\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\Rightarrow1-m^2>0\)
\(f\left(0\right)=-1< 0\)
\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=\lim\limits_{x\rightarrow-\infty}\left[\left(1-m\right)^2x^3-6x-1\right]\)
\(=\lim\limits_{x\rightarrow-\infty}x^3\left(1-m^2-\dfrac{6}{m^2}-\dfrac{1}{m^3}\right)=-\infty\left(1-m^2\right)=+\infty\) dương
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-\infty;0\right)\)
- Với \(-1< m< 1\Rightarrow1-m^2< 0\)
\(\lim\limits_{x\rightarrow+\infty}\left[\left(1-m^2\right)x^3-6x-1\right]=\lim\limits_{x\rightarrow+\infty}x^3\left[\left(1-m^2\right)-\dfrac{6}{x^2}-\dfrac{1}{x^3}\right]=+\infty\left(1-m^2\right)=+\infty\) dương
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;+\infty\right)\)
Vậy pt đã cho có nghiệm với mọi m
b. Để chứng minh pt này có đúng 1 nghiệm thì cần áp dụng thêm kiến thức 12 (tính đơn điệu của hàm số). Chỉ bằng kiến thức 11 sẽ ko chứng minh được
c.
Đặt \(f\left(x\right)=\left(m-1\right)\left(x-2\right)^2\left(x-3\right)^3+2x-5\)
Do \(f\left(x\right)\) là hàm đa thức nên \(f\left(x\right)\) liên tục trên R
\(f\left(2\right)=4-5=-1< 0\)
\(f\left(3\right)=6-5=1>0\)
\(\Rightarrow f\left(2\right).f\left(3\right)< 0\) với mọi m
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc (2;3) với mọi m
Hay pt đã cho luôn luôn có nghiệm

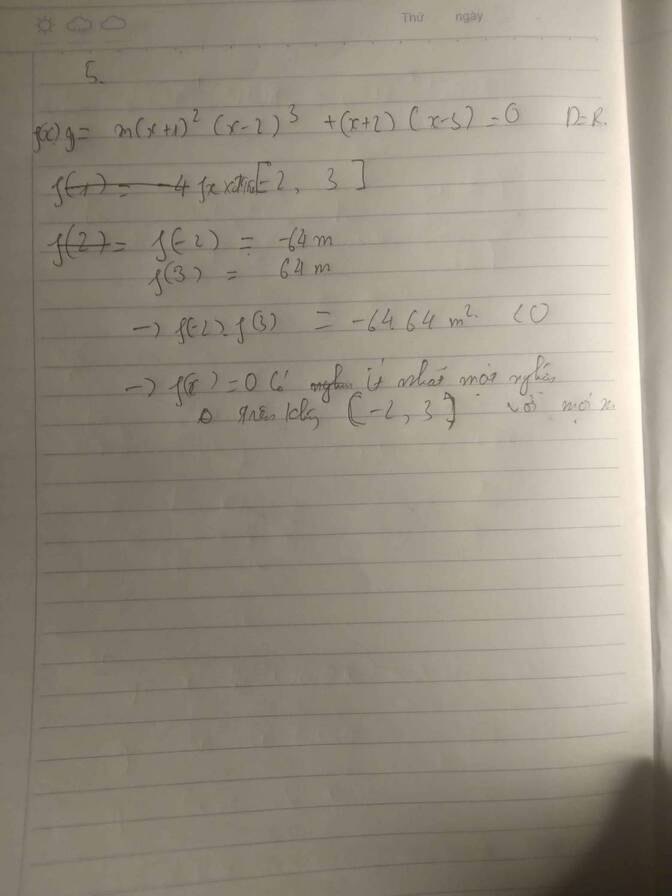
Có : \(m^2+m+1>0\) với mọi m
=> \(\left(m^2+m+1\right)x^4+2x-2=0\)là phương trình bậc 4 với mọi m
Đặt: \(f\left(x\right)=\left(m^2+m+1\right)x^4+2x-2\)
Ta có: \(f\left(0\right)=-2< 0\)với mọi m
\(f\left(1\right)=m^2+m+1>0\) với mọi m
=> Tồn tại \(a\in\left(0;1\right)\) sao cho \(f\left(a\right)=0\) với mọi m
=> Phương trình \(\left(m^2+m+1\right)x^4+2x-2=0\) có nghiệm thuộc ( 0; 1) với mọi m
=> Phương trình \(\left(m^2+m+1\right)x^4+2x-2\)=0 có nghiệm với mọi m.
Ở dòng thứ 6 bạn thêm 1 chút để chặt chẽ hơn:
Vì f(0). f(1) < 0 => tồn tại....