Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề có yêu cầu gì về các chữ số phân biệt hay không nhỉ?

Chọn A
+ Ta có ![]()
![]()
Ta có d có 4 cách chọn {2;4;6;8}, a có 9 cách chọn, b có 9 cách chọn. Vì a + b + d khi chia cho 3 có 3 khả năng số dư
{0;1;2}, mà ![]() nên c có 3 cách chọn.
nên c có 3 cách chọn.
Ta có: ![]()
Xác suất cần tìm là: 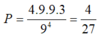

1.
Chữ số hàng đơn vị có 4 cách chọn (từ 1,3,5,7)
Chọn và hoán vị 4 chữ số từ 6 chữ số còn lại: \(A_6^4\) cách
Tổng cộng: \(4.A_6^4\) cách
2.
Gọi chữ số cần lập có dạng \(\overline{abcd}\)
a.
Lập số có 4 chữ số bất kì (các chữ số đôi một khác nhau): \(A_6^4\) cách
Lập số có 4 chữ số sao cho số 0 đứng đầu: \(A_5^3\) cách
\(\Rightarrow A_6^4-A_5^3=300\) số
b.
Để số được lập là số chẵn \(\Rightarrow\) d chẵn
TH1: \(d=0\Rightarrow abc\) có \(A_5^3\) cách chọn
TH2: \(d\ne0\Rightarrow d\) có 2 cách chọn (từ 2;4)
a có 4 cách chọn (khác 0 và d), b có 4 cách chọn, c có 3 cách chọn
\(\Rightarrow2.4.4.3=96\) số
Tổng cộng: \(A_5^3+96=156\) số
Xác suất \(P=\dfrac{156}{300}=...\)

Tổng 5 chữ số bất kì luôn \(\ge0+1+2+3+4=10\) => Mọi chữ số đề \(\le8\)
Nếu X không có 0 tổng 5 chữ số bất kì luôn \(\ge1+2+3+4+5=15\) => Mọi chữ số đều \(\le3\) ---> Vô lý
Vậy X luôn có 0 và không có 9.
Các X bộ số thỏa mãn:
+) \(\left(0;1;2;3;4;8\right)\) lập được 5.5! = 600 số tự nhiên và 5! + 3.4.4! = 408 số chẵn
+) \(\left(0;1;2;3;5;7\right)\) lập được 5.5! = 600 số tự nhiên và 5! + 4.4! = 216 số chẵn
+) \(\left(0;1;2;4;5;6\right)\) lập được 5.5! = 600 số tự nhiên và 5! + 3.4.4! = 408 số chẵn
=> Xác suất chọn được số chẵn: \(P=\dfrac{408+408+216}{600\cdot3}=\dfrac{43}{75}\)



làm đc r, ko cần nữa đâu