Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

chu vi của tam giác abc là :
ab+bc+c=25 (1)
chu vi của tam giác acd là :
ac+cd+da=27 (2)
chu vi của tứ giác abcd là :
ab+cd+bc+da=32 (3)
từ (1) và(2) ta có :
ab+bc+ac+ac+cd+da=25+27=52 (4)
=>(ab+bc+cd+da)+2ac=52
từ (1)và(4) <=>32+2ac=52
=>2ac=52-32=20
=>ac=20:2=10
vậy ac=10cm

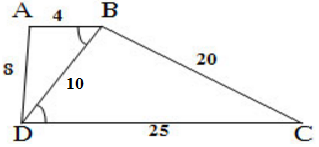
a)Vẽ tam giác BDC có BD = 10c,, DC =25cm và BC = 20cm
– Vẽ DC = 25 cm
– Vẽ đường tròn tâm D, bán kính R = 10cm và đường tròn tâm C, bán kính R = 20cm và giao điểm của 2 đường tròn trên là điểm B
* Vẽ điểm A: vẽ đường tròn tâm B, bán kính bằng 4 cm và đường tròn tâm D, bán kính bằng 8 cm. Giao điểm của hai đường tròn là A.
Tứ giác ABCD thỏa mãn các điều kiện bài toán.
b) Ta có AB/BD = 4/10 =2/5; BD/DC =10/25=2/5 và AD/BC = 8/20 =2/5
⇒ AB/BD = BD/DC = AD/BC = 2/5 ⇒ ΔABD ∽ ΔBDC
c) Ta có ΔABD ∽ ΔBDC ⇒ góc \(\widehat{ABD}=\widehat{BDC}\) ⇒ AB//DC
a) Cách vẽ:
- Vẽ ΔBDC:
+ Vẽ DC = 25cm
+ Vẽ đường tròn tâm D có bán kính = 10cm và đường tròn tâm C có bán kính = 20cm. Giao điểm của hai đường tròn là điểm B.
- Vẽ điểm A: Vẽ đường tròn tâm B có bán kính = 4cm và đường tròn tâm D có bán kính = 8cm. Giao điểm của hai đường tròn này là điểm A.
Vậy là ta đã vẽ được tứ giác ABCD thỏa mãn điều kiện đề bài.

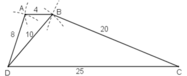
a) Cách vẽ:
- Vẽ ΔBDC:
+ Vẽ DC = 25cm
+ Vẽ cung tròn tâm D có bán kính = 10cm và cung tròn tâm C có bán kính = 20cm. Giao điểm của hai cung tròn là điểm B.
Nối DB và BC.
- Vẽ điểm A: Vẽ cung tròn tâm B có bán kính = 4cm và cung tròn tâm D có bán kính = 8cm. Giao điểm của hai cung tròn này là điểm A.
Nối DA và BA.
Vậy là ta đã vẽ được tứ giác ABCD thỏa mãn điều kiện đề bài.


A B C D 8 25 20 4 10
a, Cách vẽ :
Vẽ tam giác BDC
+) DC = 25cm
+) Vẽ cung tâm tròn D có bán kính 10cm và cung tròn tâm C có bán kính 20cm . Giao điểm của 2 cung tròn là B
- - Vẽ điểm A: Vẽ cung tròn tâm B có bán kính 4cm và cung tròn tâm D có bán kính 8cm. Giao điểm của hai cung tròn này là điểm A. Nối các cạnh BD, BC, DA, BA.
=> Vậy là ta đã vẽ được tứ giác ABCD thỏa mãn điều kiện đề bài.
b, Ta có : \(\frac{AB}{BD}=\frac{4}{10}=\frac{2}{5};\frac{BD}{DC}=\frac{10}{25};\frac{AD}{BC}=\frac{8}{20}=\frac{2}{5}\)
\(\Rightarrow\frac{AB}{BD}=\frac{BD}{DC}=\frac{AD}{BC}\)
=> tam giác ABD ∽ tam giác BDC ( c - c - c )
c, Tam giác ABD ∽ tam giác BDC ( theo chứng minh câu b )
\(\Rightarrow\widehat{ABD}=\widehat{BDC}\), mà 2 góc ở vị trí sole trong
\(\Rightarrow AB//DC\)hay ABCD là hình thang