Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2:
a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
b: ΔONP cân tại O
mà OK là trung tuyến
nên OK vuông góc NP
góc OKM=góc OAM=góc OBM=90 độ
=>O,P,A,M,B cùng nằm trên đường tròn đường kính OM
góc AKM=góc AOM
góc BKM=góc BOM
mà góc AOM=góc BOM
nên góc AKM=góc BKM
=>KM là phân giác của góc AKB

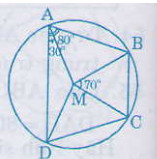
Ta có: =
-
= 80o – 30o = 50o (1)
- ∆MBC là tam giác cân (MB= MC) nên =
= 55o (2)
- ∆MAB là tam giác cân (MA=MB) nên = 50o (theo (1))
Vậy = 180o – 2. 50o = 80o
=
sđcung BCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn)
=> sđ cung BCD = 2 = 2. 80o = 160o
Mà sđ cung BC = = 70o (số đo ở tâm bằng số đo cung bị chắn)
Vậy cung DC = 160o – 70o = 90o (vì C nằm trên cung nhỏ cung BD)
Suy ra = 90o (4)
∆MAD là tam giác cân (MA= MD)
Suy ra = 180o – 2.30o = 120o (5)
∆MCD là tam giác vuông cân (MC= MD) và = 90o
Suy ra =
= 45o (6)
= 100o theo (2) và (6) và vì CM là tia nằm giữa hai tia CB, CD

Ta có: =
-
= 80o – 30o = 50o (1)
- ∆MBC là tam giác cân (MB= MC) nên =
= 55o (2)
- ∆MAB là tam giác cân (MA=MB) nên = 50o (theo (1))
Vậy = 180o – 2. 50o = 80o
=
sđcung BCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn)
=> sđ cung BCD = 2 = 2. 80o = 160o
Mà sđ cung BC = = 70o (số đo ở tâm bằng số đo cung bị chắn)
Vậy cung DC = 160o – 70o = 90o (vì C nằm trên cung nhỏ cung BD)
Suy ra = 90o (4)
∆MAD là tam giác cân (MA= MD)
Suy ra = 180o – 2.30o = 120o (5)
∆MCD là tam giác vuông cân (MC= MD) và = 90o
Suy ra =
= 45o (6)
= 100o theo (2) và (6) và vì CM là tia nằm giữa hai tia CB, CD

ˆBAD=900+12002=1050BAD^=900+12002=1050 (góc nội tiếp chắn cung BCD) (1)
ˆADC=600+9002=750ADC^=600+9002=750 ( góc nội tiếp chắn cung ABC) (2)
Từ (1) và (2) có:
ˆBAD+ˆADC=1050+750=1800BAD^+ADC^=1050+750=1800 (3)
ˆBADBAD^ và ˆADCADC^ là hai góc trong cùng phía tạo bởi cát tuyến AD và hai đường thẳng AB, CD.
Đẳng thức (3) chứng tỏ AB // CD. Do đó tứ giác ABCD là hình thang, mà hình thang nội tiếp là hình thang cân.
Vậy ABCD là hình thang cân (BC = AD và sđ cung BC = AD = 90o )
b) Giả sử hai đường chéo AC và BD cắt nhau tại I.
ˆCIDCID^ là góc có đỉnh nằm trong đường tròn, nên:
ˆCID=sđcungAB+sđcungCD2=600+12002=900CID^=sđcungAB+sđcungCD2=600+12002=900
Vậy AC ⊥ BD
c)
Vì sđ cung AB = 60o nên ˆAIB=600AIB^=600 => ∆AIB đều, nên AB = R
Vì sđ cung BC = 90o nên BC = R√2
AD = BC = R√2
nên sđ cung CD= 120o nên CD = R√3
Hướng dẫn giải:
ˆBAD=900+12002=1050BAD^=900+12002=1050 (góc nội tiếp chắn cung BCD) (1)
ˆADC=600+9002=750ADC^=600+9002=750 ( góc nội tiếp chắn cung ABC) (2)
Từ (1) và (2) có:
ˆBAD+ˆADC=1050+750=1800BAD^+ADC^=1050+750=1800 (3)
ˆBADBAD^ và ˆADCADC^ là hai góc trong cùng phía tạo bởi cát tuyến AD và hai đường thẳng AB, CD.
Đẳng thức (3) chứng tỏ AB // CD. Do đó tứ giác ABCD là hình thang, mà hình thang nội tiếp là hình thang cân.
Vậy ABCD là hình thang cân (BC = AD và sđ cung BC = AD = 90o )
b) Giả sử hai đường chéo AC và BD cắt nhau tại I.
ˆCIDCID^ là góc có đỉnh nằm trong đường tròn, nên:
ˆCID=sđcungAB+sđcungCD2=600+12002=900CID^=sđcungAB+sđcungCD2=600+12002=900
Vậy AC ⊥ BD
c)
Vì sđ cung AB = 60o nên ˆAIB=600AIB^=600 => ∆AIB đều, nên AB = R
Vì sđ cung BC = 90o nên BC = R√2
AD = BC = R√2
nên sđ cung CD= 120o nên CD = R√3

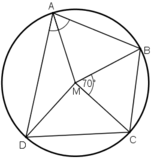
Ta có:
![]() (1)
(1)
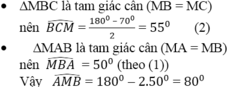 (3)
(3)
![]() (số đo góc nội tiếp bằng nửa số đo của cung bị chắn).
(số đo góc nội tiếp bằng nửa số đo của cung bị chắn).
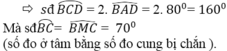
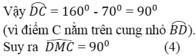
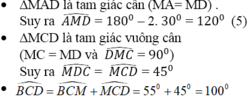
(theo (2) và (6) và Cm là tia nằm giữa hai tia CB,CD).
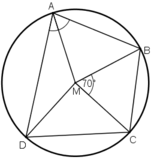


O A B C D 80
Theo tính chất góc nội tiếp, ta có:
\(\widehat{DAB}=\dfrac{1}{2}\) sđ\(\stackrel\frown{BD}\)
\(\Rightarrow\)sđ\(\stackrel\frown{BD}=2\widehat{DAB}=2.80\) độ \(=160\) độ
-Chúc bạn học tốt-