K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

HT
17 tháng 2 2021
1/ \(\overrightarrow{AM}=3\overrightarrow{AM}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\)
\(\Leftrightarrow2\overrightarrow{AM}+3\overrightarrow{MG}=\overrightarrow{0}\)
\(\Leftrightarrow2\overrightarrow{AM}+3\overrightarrow{MA}+3\overrightarrow{AG}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AM}=3\overrightarrow{AG}\)
Ban tu ket luan
2/ Bạn coi lại đề bài, đẳng thức kia có vấn đề. 2k-1IB??
17 tháng 2 2021
\(\overrightarrow{IA}+2k-1+\overrightarrow{IB}+k\overrightarrow{IC}+\overrightarrow{ID}=0\)





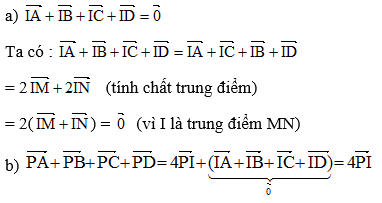
Hướng dẫn (khuya quá rồi).
Trong mp (ADN), lấy Q thuộc AD sao cho \(NP||GQ\)
\(\Rightarrow\left(\overrightarrow{MG};\overrightarrow{NP}\right)=\left(\overrightarrow{MG};\overrightarrow{GQ}\right)=180^0-\widehat{MGQ}\)
Áp dụng định lý hàm cos là tính được (\(GP=\dfrac{2}{3}NP\) ; tính MQ dựa vào hàm cos tam giác AMQ)
a có thể hướng dẫn kĩ hơn giúp e được ko ạ :(