Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
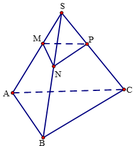
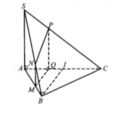
Gọi N, P là hai điểm lần lượt thuộc S B , S C thỏa mãn M N / / A B , M P / / A C .
Ta có M N // A B ⇒ M N // A B C M P // A C ⇒ M P // A B C ⇒ M N P / / A B C .
Gọi h 1 là đường cao của ΔMNP ứng với đáy MN.
Gọi h 2 là đường cao của ΔABC ứng với đáy AB.
Dễ thầy ΔMNP đồng dạng ΔABC ta có M N A B = h 1 h 2 = k .
Vậy để thỏa mãn yêu cầu bài toán
S Δ M N P S Δ A B C = 1 2 h 1 . M N 1 2 h 2 . A B = 1 2 ⇔ k . k = 1 2 ⇔ k = 2 2

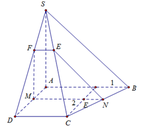
Đáp án C.


+ (ABD) và (IMK) có điểm chung là k và lần lượt chứa hai đường thẳng AB // MI
=>Giao tuyến của (ABD) và (IMK) là đường thẳng đi qua K và song song với AB và AD tại E =>Thiết diện cần tìm là tứ giác MKEI có M I / / K E M I > K E (1)
+ Δ B M K = Δ A I E ⇒ I E = M K (2)
Từ (1) và (2) =>Tứ giác MKEI là hình thang cân với đáy lớn là MI
+ Có E K = 1 3 ; A B = a 3 ; M I = a 2
Gọi H là hình chiếu vuông góc của E lên MI =>2IH + EK = IM => I H = a 12
I E = A I 2 + A E 2 − 2 A I . A E . c o s 60 ° = a 13 6 ⇒ E H = 13 a 2 36 − a 2 144 = a 51 12
S I M K E = 1 2 E K + I M . E H = 5 a 2 51 144

Đáp án A
Hiển nhiên thiết diện của hình tứ diện A B C D khi cắt bởi mặt phẳng M N P là một tam giác

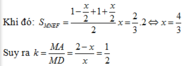
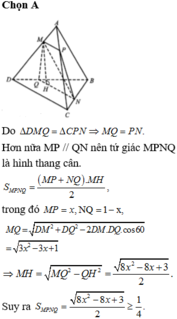
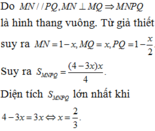
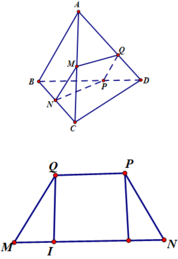

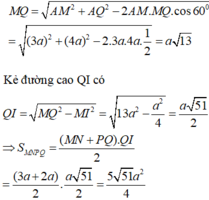
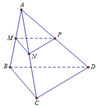
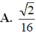
Đáp án C
Xét trường hợp A P P C = k , lúc này M P // B C nên B C // M N P .
Ta có: N ∈ M N P ∩ B C D B C // M N P B C ⊂ B C D ⇒ B C D ∩ M N P = N Q // B C , Q ∈ B D .
Thiết diện là tứ giác MPNQ.
Xét trường hợp A P P C ≠ k .
Trong A B C gọi R = B C ∩ M P .
Trong B C D gọi Q = N R ∩ B D thì thiết diện là tứ giác MNPQ.
Gọi K = M N ∩ P Q . Ta có S M N P S M N P Q = P K P Q .
Do A M N B = C N N D nên theo định lí Thales đảo thì A C , N M , B D lần lượt thuộc ba mặt phẳng song song với nhau và đường thẳng PQ cắt ba mặt phẳng này tương ứng tại P, K, Q nên áp dụng định lí Thales ta được P K K Q = A M M B = C N N D = k
⇒ P K P Q = P K P K + K Q = P K K Q P K K Q + 1 = k k + 1