Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong mp (ACD), kéo dài IJ cắt CD tại E thì E là giao điểm của CD và (IJK)

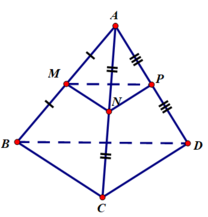
Vì M, N, P lần lượt là trung điểm của AB, AC, AD nên MN, NP, MP lần lượt là đường trung bình của tam giác ABC, ACD, ABD
⇒ MN//BC, NP//CD, PM //BD
Mà BC, CD, BD thuộc (BCD)
MN, NP, PM không thuộc (BCD)
⇒ Các đường thẳng MN, NP, PM có song song với mặt phẳng (BCD)

△ABC có: M, N là trung điểm của AB, AC
Suy ra: MN // BC nên MN // (BCD).
△ACD có: N, P là trung điểm của AC, AD
Suy ra: NP // CD nên NP // (BCD).
△ABD có: M, P là trung điểm của AB, AD
Suy ra: MP // BD nên MP // (BCD).
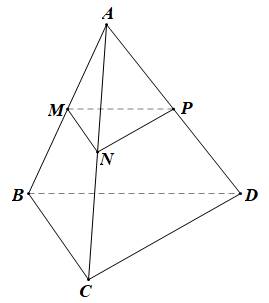
• Xét DABC có M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của tam giác
Do đó MN // BC
Lại có BC ⊂ (BCD)
Suy ra MN // (BCD).
• Chứng minh tương tự ta cũng có NP // CD.
Mà CD ⊂ (BCD)
Suy ra NP // (BCD).
• Tương tự, MP // BD mà BD ⊂ (BCD) .
Suy ra MP // (BCD).

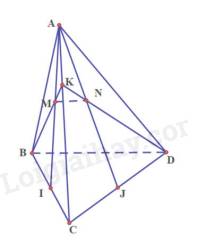
Giả sử K là trung điểm của AC
Suy ra M,N lần lượt là trọng tâm của tam giác ABC và tam giác ACD
Do đó, tam giác KBC có:\(\frac{{KM}}{{KB}} = \frac{{KN}}{{KD}} = \frac{1}{3}\)
Suy ra MN // BD
Chứng minh tương tự với trường hợp K bất kỳ

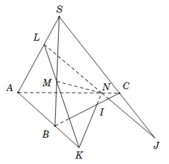
Ta có
+ M thuộc SB suy ra M là điểm chung của (LMN) và ( SBC) .
+ I là điểm chung của (LMN) và (SBC)
+ J là điểm chung của (LMN) và (SBC) .
Vậy M; I; J thẳng hàng vì cùng thuộc giao tuyến của (LMN) và (SBC).
Chọn B.

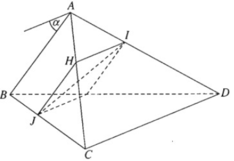
Qua I kẻ đường thẳng song song với CD cắt AC tại H, ta có:
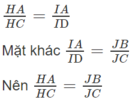
Suy ra HJ // AB
Như vậy mặt phẳng (IJH) song song với AB và CD.
Gọi (α) là mặt phẳng qua AB và song song với CD, ta có
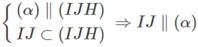
Vậy IJ song song với mặt phẳng (α) cố định.

Đáp án B
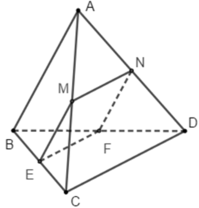
Mặt phẳng α chứa MN song song với AB
Gọi E và F lần lượt là trung điểm của BC và BD
Tam giác ABC có EM là đường trung bình nên ME // = 1/2 AB
Tam giác ABD có FN là đường trung bình nên FN // = 1/2 AB
Suy ra ME // FN // AB và ME = FN
Hay mặt phẳng (MNFE) chính là mặt phẳng α
Vậy thiết diện của mặt phẳng α với tứ diện là hình bình hành MNFE (do ME // = FN)