
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tập A có n phần tử:
Số tập con có 3 phân tử là: \(C_n^3=\frac{n!}{3!\left(n-3\right)!}=\frac{n\left(n-1\right)\left(n-2\right)}{6}\)
Số tập con 2 phần tử là : \(C_n^2=\frac{n!}{2!\left(n-2\right)!}=\frac{n\left(n-1\right)}{2}\)
Theo bài ra ta có: \(\frac{n\left(n-1\right)\left(n-2\right)}{6}-\frac{n\left(n-1\right)}{2}=14\)<=> \(n^3-6n^2+5n-84=0\Leftrightarrow n=7\)
Vậy tập A có 7 phần tử

Tập A có các tập con là:
+) tập hợp rỗng.
+) 3 tập con có 1 phần tử là: {a}, {b}, {c}
+) 3 tập con có 2 phần tử là: {a;b}, {b;c}, {c;a}
+) 1 tập con có 3 phần tử: {a;b;c} (là tập A)
Vậy tập A có 1+3+3+1=8 tập hợp con.
Chọn C.
Chú ý khi giải
+ Khi tính số tập hợp con, mọi tập A luôn có 2 tập con là tập \(\emptyset \) và chính nó.
+ Số tập hợp con của tập hợp A có n phần tử là: \({2^n}\)

\(B\cap D=A\\ \Rightarrow D=\left\{0;1;2;3\right\}\\ D=\left\{0;1;2;3;5\right\}\\ D=\left\{0;1;2;3;5;7\right\}\)
Có 3 tập hợp D thỏa mãn

Các tập con của tập hợp B là:
+) Tập con có 0 phần tử: \(\emptyset \) (tập hợp rỗng)
+) Các tập hợp con có 1 phần tử: {0}, {1}, {2}
+) Các tập hợp con có 2 phần tử: {0;1}, {1;2}, {0;2}
+) Tập hợp con có 3 phần tử: \(B = \{ 0;1;2\} .\)
Chú ý
+) Mọi tập hợp B đều có 2 tập con là: \(\emptyset \) và B.
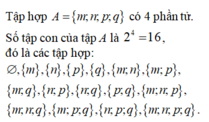

`A` có `8` tập con đó là:
{\(\emptyset\)} ; {`0`} ; {`1`} ; {`2`} ; {`0;1`} ; {`0;2`} ; {`1;2`} ; {`0;1;2`}
Tập con có không phân tử là : \(\varnothing\)
Có 1 phần tử : \(\left\{0\right\};\left\{1\right\}:\left\{2\right\}\)
có 2 phần tử : \(\left\{1;0\right\};\left\{2;0\right\};\left\{1;2\right\}\)
có 3 phần tử : \(\left\{1;0;2\right\}\)
=> tập A có 8 tập con