Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
2/Xét ∆ABD và ∆ACE có:
b.
Xét ∆HDC và ∆HEB có:
\(\frac{HD}{HE}=\frac{HC}{HB}< =>HD.HB=HE.HC\)
c.Vì H là giao điểm của 2 đường cao CE,BD 
Xét ∆CIF và ∆CFA có:
a
Xét \(\Delta EBH\) và \(\Delta DHC\) có:
\(\widehat{EHB}=\widehat{DHC}\left(đ.đ\right)\)
\(\widehat{E}=\widehat{D}=90^0\)
\(\Rightarrow\Delta EBH~\Delta DHC\left(g.g\right)\)
b
\(\frac{S_{ABF}}{S_{ACF}}=\frac{\frac{AF\cdot BF}{2}}{\frac{AF\cdot CF}{2}}=\frac{BF}{CF}\)
Tuong tu ta co:
\(\frac{S_{ABD}}{S_{CBD}}=\frac{DA}{DC}\)
\(\frac{S_{BCE}}{S_{ACE}}=\frac{EB}{EA}\)
Nhan ve theo ve ta co dpcm
A B C D E F H
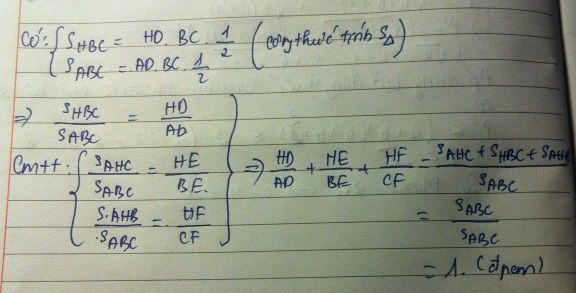
Với \(AF;\) \(BD;\) \(CE\) lần lượt là ba đường cao ứng với các cạnh \(BC;\) \(AC;\) \(AB\) của \(\Delta ABC\), ta có:
\(\frac{S_{BHC}}{S_{ABC}}=\frac{\frac{1}{2}.HF.BC}{\frac{1}{2}.AF.BC}=\frac{HF}{AF}\) \(\left(1\right)\)
\(\frac{S_{AHC}}{S_{ABC}}=\frac{\frac{1}{2}.HD.AC}{\frac{1}{2}.CD.AC}=\frac{HD}{CD}\) \(\left(2\right)\)
\(\frac{S_{AHB}}{S_{ABC}}=\frac{\frac{1}{2}.HE.AB}{\frac{1}{2}.BE.AB}=\frac{HE}{BE}\) \(\left(3\right)\)
Cộng từng vế \(\left(1\right);\) \(\left(2\right)\) và \(\left(3\right)\), với chú ý rằng \(S_{BHC}+S_{AHC}+S_{AHB}=S_{ABC}\), ta được:
\(\frac{HF}{AF}+\frac{HD}{CD}+\frac{HE}{BE}=\frac{S_{BHC}+S_{AHC}+S_{AHB}}{S_{ABC}}=\frac{S_{ABC}}{S_{ABC}}=1\)
Vậy, ....