Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
góc EAH+góc ACB=90 độ
góc EBC+góc ACB=90 độ
=>góc EAH=góc EBC
b: AK cắt EF tại M
AK cắt BC tại N
AH cắt (O) tại K
=>HM//AB và QN//AB
=>HM//QN

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: Xet ΔBDH vuông tại D và ΔBEC vuông tại E có
góc DBH chung
=>ΔBDH đồng dạng với ΔBEC
=>BH/BC=DH/EC
=>BH*EC=DH*BC

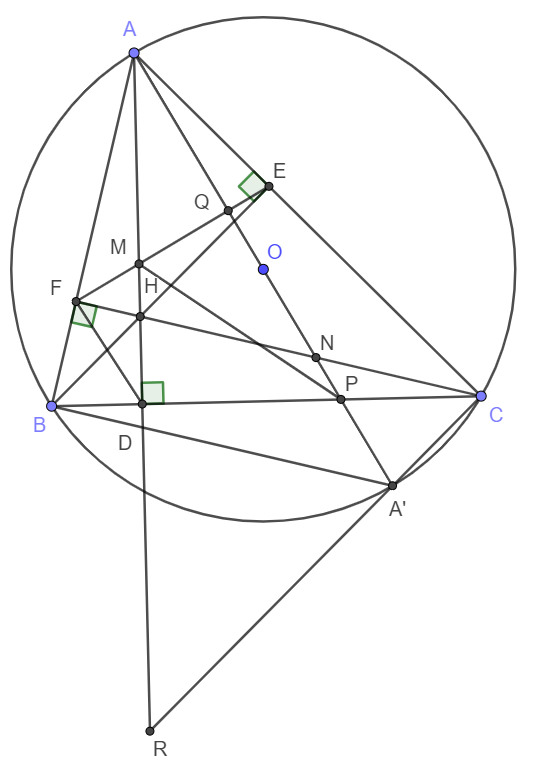
a) theo gt, BFC=BEC=90
=> BFEC nội tiếp (có 2 góc kề bang nhau)
góc AFC=ADC=90 => AFDC nội tiếp ( có 2 cạnh kề cùng nhìn một đoan thẳng bằng nhau)
b) vì tứ giác ABA'C nội tiếp => ABC = AA'C (cùng chắn cung AC)
Lại có ABC= AHF (Cùng phụ với góc BAD)
Ta thấy AFHE nội tiếp vì AFH +AEH = 90+90=180
=> AHF=AEF (Cùng chắn cung AF)
=>Đpcm
c) vì tứ giác EQA'C nôi tiếp
nên EQA'+ECA'=180 mà ECA'=90 vì là góc nội tiếp chắn nửa đường tròn
=> MQP=EQA'=90 ( vì MQP+EQA=180)
Trong đó ADC=90 =>Đpcm
d) Vì ABA'C VÀ FBDH nội tiếp nên góc NA'C=ABC=DHC
=>NA'C=DHC=>Đpcm
a) Chứng minh ADEH là tứ giác nội tiếp.Ta có: ∠ADB=900 (góc nội tiếp chắn nửa đường tròn)EH⊥AB⇒∠AHE=900Tứ giác ADEH có: ∠ADE+∠AHE=900+900=1800 nên là tứ giác nội tiếp (đpcm)b) Tia CH cắt đường tròn (O) tại điểm thứ hai là K. Gọi I là giao điểm của DK và AB. Chứng minh DI2=AI.BI.Tứ giác ADCK nội tiếp nên ∠ADK=∠ACK (hai góc nội tiếp cùng chắn cung AK) (1)Xét tứ giác ECBH có:∠ECB=∠ACB=900 (góc nội tiếp chắn nửa đường tròn)∠EHB=900(doEH⊥AB)⇒∠ECB+∠EHB=900+900=1800Do đó tứ giác ECBH nội tiếp (tứ giác có hai góc đối có tổng số đo bằng 1800)⇒∠ECH=∠EBH (hai góc nội tiếp cùng chắn cung EH)⇒∠ACK=∠DBA (2)Từ (1) và (2) suy ra ∠ADK=∠DBA⇒∠ADI=∠DBALại có ∠DBA+∠DAB=900 nên ∠ADI+∠DAB=900 hay ∠ADI+∠DAI=900⇒∠DIA=1800−(∠ADI+∠DAI)=1800−900=900⇒DI⊥AB nên DI là đường cao trong tam giác vuông ADB⇒DI2=IA.IB (hệ thức giữa cạnh và đường cao trong tam giác vuông) (đpcm)c) Khi tam giác DAB không cân, gọi M là trung điểm của EB, tia DC cắt tia HM tại N. Tia NB cắt đường tròn ngoại tiếp tam giác HMB tại điểm thứ hai là F. Chứng minh F thuộc đường tròn (O).Theo câu b, DK⊥BA tại I nên AB là đường trung trực của DK⇒DA=AK ⇒sdcungAD=sdcungAK⇒∠DCA=∠ACK ⇒CA là tia phân giác của góc ∠DCH⇒∠DCH=2∠ECH (3)Tam giác EHB vuông tại H có M là trung điểm EB nên HM là đường trung tuyến⇒MH=MB⇒ΔMHB cân tại M⇒∠DMH=∠MHB+∠MBH=2∠MBH=2∠EBH (4)Tứ giác ECBH có: ∠ECB+∠EHB=900+900=1800 nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng 1800)⇒∠ECH=∠EBH (5)Từ (3), (4) và (5) suy ra ∠DCH=∠DMH⇒DCMH là tứ giác nội tiếp (hai đỉnh kề nhau cùng nhìn cạnh đối diện các góc bằng nhau)⇒∠NCM=∠NHD (tính chất)Xét ΔNCM và ΔNHD có:Góc N chung∠NCM=∠NHD(cmt)⇒ΔNCM∼ΔNHD(g−g)⇒NCNH=NMND (cạnh tương ứng)⇒NC.ND=NM.NH (6)Tứ giác HMBF nội tiếp nên ∠NMB=∠NFH (tính chất)Xét ΔNMB và ΔNFH có:Góc N chung∠NMB=∠NFH (cmt)⇒ΔNMB∼ΔNFH(g−g)⇒NMNF=NBNH (cạnh tương ứng)⇒NM.NH=NB.NF (7)Từ (6) và (7) suy ra NC.ND=NF.NB⇒NCNF=NBNDXét ΔNBC và ΔNDF có:Góc N chungNCNF=NBND(cmt)⇒ΔNBC∼ΔNDF(c−g−c)⇒∠NCB=∠NFD=∠BFD (góc tương ứng)Mà ∠NCB+∠DCB=1800 (kề bù)Nên ∠BFD+∠DCB=1800Do đó tứ giác DCBF nội tiếp (tứ giác có tổng hai góc đối bằng 1800)Vậy điểm F nằm trên đường tròn (O) (đpcm).